What Is A 9 Sided Polygon
Juapaving
Mar 25, 2025 · 6 min read
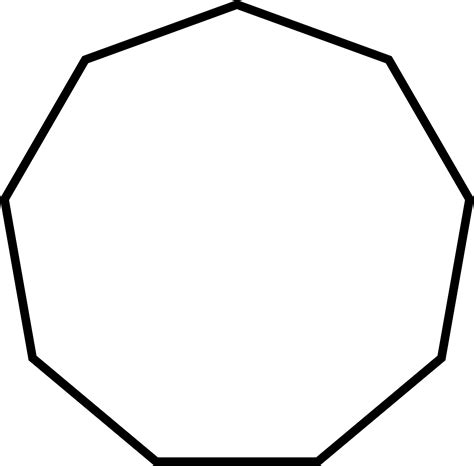
Table of Contents
What is a 9-Sided Polygon? A Deep Dive into Nonagons
A polygon, in simple terms, is a closed two-dimensional figure formed by connecting straight line segments. The number of sides determines the polygon's name and properties. Today, we're delving into the fascinating world of nonagons, also known as enneagons, nine-sided polygons. This comprehensive guide will cover everything from basic definitions and properties to advanced concepts and applications, ensuring you gain a thorough understanding of this often-overlooked geometric shape.
Understanding the Basics: Defining a Nonagon
A nonagon (or enneagon) is a polygon with nine sides and nine angles. Its name derives from the Greek words "ennea" (meaning nine) and "gonia" (meaning angle). Like all polygons, nonagons can be classified based on their regularity and the lengths of their sides and the measures of their angles.
Regular vs. Irregular Nonagons
-
Regular Nonagon: A regular nonagon has all nine sides of equal length and all nine angles of equal measure. Each interior angle of a regular nonagon measures 140 degrees, and each exterior angle measures 40 degrees. The sum of the interior angles of any nonagon, regular or irregular, is always 1260 degrees. This is calculated using the formula (n-2) * 180, where 'n' represents the number of sides. In the case of a nonagon, (9-2) * 180 = 1260 degrees.
-
Irregular Nonagon: An irregular nonagon has sides of varying lengths and angles of varying measures. The only consistent property is the sum of its interior angles, which remains 1260 degrees.
Exploring the Properties of Nonagons
Beyond the basic definition, several key properties define and differentiate nonagons:
1. Interior Angles:
As mentioned, the sum of the interior angles of any nonagon is 1260 degrees. In a regular nonagon, each interior angle measures 140 degrees (1260/9 = 140). However, in an irregular nonagon, the individual angles will vary, but their sum will always be 1260 degrees.
2. Exterior Angles:
The sum of the exterior angles of any polygon, including a nonagon, always equals 360 degrees. In a regular nonagon, each exterior angle measures 40 degrees (360/9 = 40). The exterior angles of an irregular nonagon will also vary, but their sum remains constant at 360 degrees.
3. Diagonals:
A diagonal is a line segment connecting two non-adjacent vertices of a polygon. A nonagon has 27 diagonals. This can be calculated using the formula n(n-3)/2, where 'n' is the number of sides. For a nonagon (n=9), the calculation is 9(9-3)/2 = 27. These diagonals create various triangles and smaller polygons within the nonagon, aiding in area calculations and geometrical analyses.
4. Symmetry:
A regular nonagon possesses rotational symmetry of order 9, meaning it can be rotated 40 degrees (360/9 = 40) about its center and still look identical. It also has nine lines of reflectional symmetry, each passing through a vertex and the midpoint of the opposite side. Irregular nonagons may possess some symmetry, but not to the same extent as regular nonagons.
5. Area Calculation:
Calculating the area of a regular nonagon is more complex than that of simpler polygons. One method involves dividing the nonagon into nine congruent isosceles triangles, each with one vertex at the center of the nonagon. The area of each triangle can be calculated, and then multiplied by nine to find the total area. For irregular nonagons, the area calculation is more intricate and often requires advanced techniques like triangulation or the use of coordinate geometry. Formulas using the side length (s) and apothem (a) (the distance from the center to the midpoint of a side) are also available, though their derivation is beyond the scope of this introductory article.
Nonagons in Real-World Applications and Examples
While not as commonly encountered as triangles, squares, or hexagons, nonagons appear in various real-world applications and natural phenomena, often in subtle ways:
1. Architecture and Design:
Though not as prevalent as other polygons, nonagons can be found in architectural designs, albeit infrequently. Specific buildings might incorporate nonagonal elements in their floor plans, windows, or decorative features. The unusual shape can add a unique aesthetic touch.
2. Nature and Geometry:
Certain natural formations might exhibit approximate nonagonal shapes, although perfect regularity is rare in nature. Crystal structures, for instance, can sometimes display patterns with nine-fold symmetry, though these are often variations on the theme rather than perfectly regular nonagons.
3. Tessellations:
While a regular nonagon cannot tessellate (tile a plane without gaps), certain combinations of nonagons and other polygons can create intriguing tessellation patterns. Exploring these possibilities can lead to visually appealing designs in art and crafts.
4. Engineering and Construction:
Specialized engineering or construction projects might utilize nonagonal structures for specific purposes, though these applications are often niche and context-dependent. Think of unique designs for machinery parts or specific architectural installations.
5. Art and Crafts:
Artists and craftspeople may incorporate nonagonal shapes into their work for their unique visual impact. From creating geometric patterns in quilting to designing custom jewelry, the possibilities are numerous.
Beyond the Basics: Advanced Concepts Related to Nonagons
The study of nonagons can extend beyond basic geometry into more advanced mathematical concepts:
1. Constructions:
Constructing a regular nonagon using only a compass and straightedge is not possible, as 9 is not a Fermat prime (a prime number of the form 2<sup>(2<sup>n</sup>)</sup> + 1). This is a significant difference compared to some other polygons, like pentagons and hexagons, which can be constructed using these tools. However, approximate constructions can be achieved using various techniques.
2. Star Nonagons:
By connecting vertices of a nonagon in a non-adjacent manner, you can create star polygons, such as a nonagram {9/2} or {9/4}. These figures exhibit a distinct visual appeal due to their interlacing lines.
3. Nonagonal Numbers:
In number theory, nonagonal numbers are figurate numbers that represent the number of dots arranged in a regular nonagon. The nth nonagonal number is given by the formula: n(7n-5)/2.
4. Nonagon in Higher Dimensions:
The concept of a nonagon can be extended to higher dimensions. Imagine a nine-sided figure existing in three-dimensional space—a more complex geometrical entity. The mathematical description and analysis of these higher-dimensional analogues become considerably more intricate.
Conclusion: A Deeper Appreciation for the Nonagon
While often overshadowed by more commonly known polygons, the nonagon offers a rich field of study for both beginners and advanced mathematicians. From understanding its basic properties to exploring its advanced applications, the nonagon demonstrates the beauty and complexity inherent in geometric shapes. Whether you're a student, a teacher, an artist, or simply curious about mathematics, understanding the intricacies of the nine-sided polygon provides a rewarding exploration into the world of geometry. The unique combination of its properties and its relatively infrequent occurrence makes it a particularly fascinating object of study, pushing the boundaries of our geometric understanding and providing fertile ground for creative exploration in various fields.
Latest Posts
Latest Posts
-
5 Letter Word Ending In At
Mar 29, 2025
-
Diagram Of An Animal And Plant Cell
Mar 29, 2025
-
What Is The Difference Between Environment And Ecosystem
Mar 29, 2025
-
How To Find Average Speed With Two Speeds
Mar 29, 2025
-
A Subset Of A Population Is Called A
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is A 9 Sided Polygon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
