What Is 1.625 In Fraction Form
Juapaving
Mar 28, 2025 · 4 min read
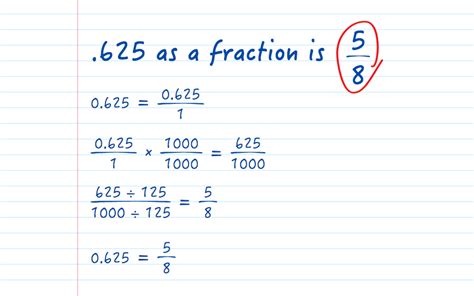
Table of Contents
What is 1.625 in Fraction Form? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but with a systematic approach, it becomes a straightforward process. This comprehensive guide will walk you through converting the decimal 1.625 into its fractional equivalent, explaining the underlying principles and offering additional tips for similar conversions. We'll explore various methods, ensuring you understand not just the answer but also the why behind it.
Understanding Decimal to Fraction Conversion
Before diving into the conversion of 1.625, let's establish the fundamental principles. A decimal represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). The conversion process involves identifying the place value of the last digit and using that to determine the denominator.
Breaking Down the Decimal: 1.625
The decimal 1.625 comprises:
- 1: This represents one whole unit.
- .625: This is the fractional part. The last digit, 5, is in the thousandths place.
Method 1: Using the Place Value
Since the last digit (5) is in the thousandths place, we can express 0.625 as a fraction with a denominator of 1000:
0.625 = 625/1000
This fraction, however, can be simplified.
Method 2: Simplifying the Fraction
Simplifying a fraction means reducing it to its lowest terms. We achieve this by finding the greatest common divisor (GCD) of the numerator (625) and the denominator (1000) and dividing both by it.
Finding the GCD can be done using several methods:
- Prime Factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- Euclidean Algorithm: A more efficient method for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Let's use prime factorization for 625 and 1000:
- 625: 5 x 5 x 5 x 5 = 5⁴
- 1000: 2 x 2 x 2 x 5 x 5 x 5 = 2³ x 5³
The common prime factor is 5, and the lowest power is 5³. Therefore, the GCD is 5³ = 125.
Dividing both the numerator and the denominator by 125:
625 ÷ 125 = 5
1000 ÷ 125 = 8
This simplifies our fraction to 5/8.
Method 3: Combining the Whole Number and Fraction
Remember, our original decimal was 1.625. We now have the fractional part as 5/8. To combine this with the whole number (1), we simply add them:
1 + 5/8 = 1 5/8
Therefore, 1.625 in fraction form is 1 5/8.
Alternative Method: Using a Calculator
While understanding the underlying principles is crucial, you can also use a calculator to convert decimals to fractions. Many calculators have a built-in function for this. However, it's still beneficial to understand the manual process, especially for more complex conversions or when a calculator isn't available.
Converting Other Decimals to Fractions
The methods described above can be applied to other decimals. Here are a few examples:
-
0.75: The last digit is in the hundredths place, so we represent it as 75/100. Simplifying this by dividing both the numerator and denominator by 25 gives us 3/4.
-
0.375: The last digit is in the thousandths place, so it's 375/1000. The GCD is 125, resulting in 3/8.
-
2.25: This is 2 + 0.25 = 2 + 25/100 = 2 + 1/4 = 2 1/4 or 9/4
Practical Applications of Decimal to Fraction Conversion
Understanding decimal to fraction conversions is crucial in various fields:
- Cooking and Baking: Recipes often require precise measurements, and fractions are commonly used.
- Construction and Engineering: Accurate measurements are vital in construction, and fractions are used extensively in blueprints and calculations.
- Mathematics and Science: Fraction representation is fundamental in various mathematical and scientific computations.
- Finance: Fractions are used to represent percentages and ratios in financial calculations.
Troubleshooting Common Mistakes
- Incorrect Place Value: Make sure to accurately identify the place value of the last digit in the decimal. This is the key to determining the correct denominator.
- Incomplete Simplification: Always simplify the fraction to its lowest terms. This ensures the most accurate and concise representation.
- Ignoring the Whole Number: Remember to add the whole number back to the simplified fraction when dealing with mixed decimals.
Conclusion: Mastering Decimal to Fraction Conversions
Converting decimals like 1.625 to fractions involves a combination of understanding place value, simplifying fractions using GCD, and combining whole numbers with fractional parts. While calculators can assist, a thorough understanding of the process empowers you to perform these conversions confidently and accurately in any situation. Mastering this skill enhances your mathematical proficiency and opens doors to more complex calculations across various fields. Remember to practice regularly and utilize different methods to solidify your understanding. With consistent effort, you'll become adept at converting decimals to fractions and handling related mathematical tasks with ease.
Latest Posts
Latest Posts
-
Mass Of An Electron In Mev
Mar 31, 2025
-
From A Gas To A Liquid
Mar 31, 2025
-
How Many Feet Is 16 Meters
Mar 31, 2025
-
Examples Of Gas To A Liquid
Mar 31, 2025
-
Horizontal Cross Section Of A Cone
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 1.625 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
