What Does Complementary Mean In Geometry
Juapaving
Mar 29, 2025 · 6 min read
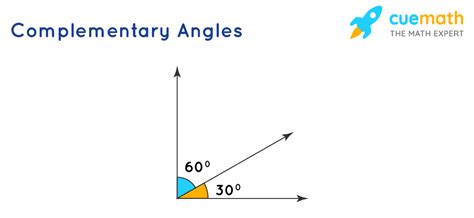
Table of Contents
What Does Complementary Mean in Geometry? A Deep Dive into Angles and Their Relationships
In the fascinating world of geometry, understanding the relationships between different shapes and figures is key to unlocking deeper mathematical concepts. One such fundamental relationship involves angles and their complementary nature. This article delves into the precise meaning of "complementary" in geometry, exploring its definition, applications, and significance in various geometric problems and theorems. We will also examine related concepts and provide numerous examples to solidify your understanding.
Defining Complementary Angles: The Core Concept
In geometry, complementary angles are defined as two angles whose measures add up to 90 degrees (a right angle). It's crucial to understand that these angles don't have to be adjacent; they simply need to satisfy the sum condition. This simple yet powerful definition forms the basis for numerous geometrical proofs and problem-solving techniques. The term "complementary" implies a relationship of mutual completion, where one angle "complements" the other to form a right angle.
Key Characteristics of Complementary Angles:
- Sum of 90 degrees: This is the defining characteristic. If the sum of two angles is not 90 degrees, they are not complementary.
- Not necessarily adjacent: Complementary angles can be located anywhere in a geometrical figure; their spatial relationship is irrelevant to their complementary nature.
- Can be of different measures: The only requirement is that their sum is 90 degrees. They could be two equal 45-degree angles or a 10-degree angle and an 80-degree angle – both pairs are complementary.
Identifying Complementary Angles in Diagrams and Problems
Identifying complementary angles in geometric diagrams requires careful observation and application of the definition. Look for angles that, when combined, appear to form a right angle. However, it is vital to rely on the numerical values provided or derived from the diagram. Visual estimation alone can be unreliable.
Let's examine some typical scenarios:
-
Right-angled triangles: In a right-angled triangle, the two acute angles are always complementary. This is a direct consequence of the angle sum property of triangles (the sum of angles in a triangle is always 180 degrees). Since one angle is 90 degrees, the remaining two must add up to 90 degrees.
-
Intersecting lines: When two lines intersect, they form four angles. Pairs of angles opposite each other are called vertical angles and are always equal. Adjacent angles formed by intersecting lines are supplementary (their sum is 180 degrees). Within these intersecting lines, you might find complementary angle pairs.
-
Geometric constructions: Many geometric constructions, such as bisecting an angle or constructing a perpendicular, implicitly or explicitly involve complementary angles. Understanding their presence and properties is essential in these constructions.
Complementary Angles: Applications and Examples
The concept of complementary angles finds extensive applications throughout geometry and related fields. Understanding complementary angles is crucial for solving various geometrical problems. Let's delve into some practical examples:
Example 1: Simple Angle Calculation
If angle A measures 35 degrees, and angle A and angle B are complementary, what is the measure of angle B?
Solution: Since angles A and B are complementary, their sum is 90 degrees. Therefore, angle B = 90 degrees - 35 degrees = 55 degrees.
Example 2: Problem Solving in Right-Angled Triangles
A right-angled triangle has one acute angle of 28 degrees. Find the measure of the other acute angle.
Solution: In a right-angled triangle, the two acute angles are complementary. Therefore, the other acute angle is 90 degrees - 28 degrees = 62 degrees.
Example 3: Complementary Angles in Intersecting Lines
Two lines intersect, forming four angles. One angle measures 60 degrees. Identify the complementary angle(s).
Solution: The angle opposite the 60-degree angle also measures 60 degrees (vertical angles). The adjacent angles to the 60-degree angle are supplementary (180 degrees - 60 degrees = 120 degrees). There is no complementary angle directly adjacent to the 60-degree angle within this intersection. However, consider the situation where another line bisects the 120-degree angle. In such a case, two 30-degree angles would result, which would be complementary to the 60-degree angle.
Example 4: Application in Trigonometry
Trigonometric functions, such as sine, cosine, and tangent, are heavily reliant on the relationships between angles in a right-angled triangle. The complementary relationship between the acute angles is fundamental in deriving trigonometric identities and solving trigonometric equations. For instance, sin(x) = cos(90° - x), showcasing the link between complementary angles and trigonometric functions.
Complementary Angles and Their Relationship with Other Angle Relationships
Complementary angles are closely related to other angle relationships, particularly supplementary angles. Understanding these relationships enhances your geometrical problem-solving skills.
Supplementary Angles: A Comparison
Supplementary angles are two angles whose sum is 180 degrees. This is a crucial distinction from complementary angles, which sum to 90 degrees. While complementary angles always involve acute angles (less than 90 degrees), supplementary angles can involve acute, obtuse (greater than 90 degrees but less than 180 degrees), or a combination of both. The key difference lies in the sum of the angles.
Adjacent Angles: A Consideration
While complementary angles can be adjacent (sharing a common vertex and side), they don't have to be. Adjacent angles are simply angles that share a common vertex and side. Many adjacent angles are supplementary, but not all. The concept of adjacency is separate from the relationship defined by the sum of the angles.
Advanced Applications and Problem Solving with Complementary Angles
The application of complementary angles extends beyond basic geometrical problems. They play a significant role in:
-
Coordinate geometry: Complementary angles are often used to find angles between lines and calculate distances. Understanding the relationship between the slope of a line and its angle with the x-axis is crucial in coordinate geometry, and this often involves complementary angles.
-
Calculus: In calculus, the concept of complementary angles appears in various applications, particularly when dealing with trigonometric functions and their derivatives.
-
Engineering and architecture: The principles of complementary angles are vital in various engineering and architectural designs, ensuring structural stability and accurate measurements.
Conclusion: Mastering Complementary Angles in Geometry
Understanding the concept of complementary angles is paramount for anyone seeking to master geometry. This article has detailed the definition, characteristics, and applications of complementary angles, emphasizing their importance in various geometrical problems and theorems. By practicing the examples and exploring the advanced applications, you can solidify your understanding and improve your ability to solve a wide range of geometrical problems. The core takeaway is that while seemingly simple, the concept of complementary angles forms a building block for more complex geometrical concepts and real-world applications. Remember to always rely on precise measurements and logical reasoning, rather than visual estimation alone, when working with angles. With consistent practice and a clear understanding of the fundamentals, you'll find yourself confidently navigating the fascinating world of geometry and its intriguing relationships.
Latest Posts
Latest Posts
-
How Do You Spell 90 In Word Form
Apr 01, 2025
-
200 Is What Percent Of 50
Apr 01, 2025
-
What Is 15 Percent Of 250
Apr 01, 2025
-
Temperature And Kinetic Energy Are Proportional
Apr 01, 2025
-
What 2 Subatomic Particles Make Up The Nucleus
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Does Complementary Mean In Geometry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
