What Are The Prime Factors Of 420
Juapaving
Mar 31, 2025 · 5 min read
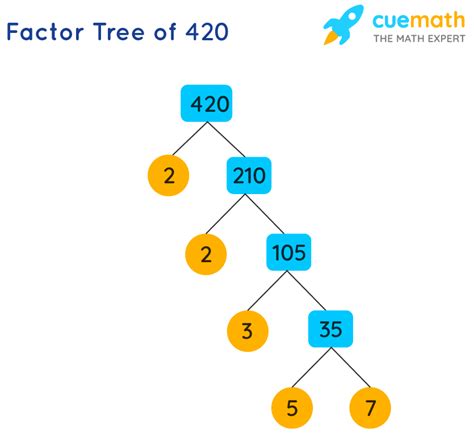
Table of Contents
What Are the Prime Factors of 420? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but understanding the process reveals fundamental concepts in number theory and has practical applications in various fields, from cryptography to computer science. This article will thoroughly explore how to find the prime factors of 420, explaining the method, demonstrating the steps, and delving into the broader significance of prime factorization.
Understanding Prime Numbers and Prime Factorization
Before we delve into the specifics of 420, let's establish a firm understanding of the core concepts.
Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves. Examples include 2, 3, 5, 7, 11, and so on. These numbers are the building blocks of all other whole numbers.
Prime factorization is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. Every composite number can be uniquely expressed as a product of primes, regardless of the order of the factors. This is known as the Fundamental Theorem of Arithmetic.
Finding the Prime Factors of 420: A Step-by-Step Guide
Now, let's break down the process of finding the prime factors of 420. We can use a method known as the factor tree.
-
Start with the smallest prime number: The smallest prime number is 2. Since 420 is an even number, it's divisible by 2.
420 = 2 × 210
-
Continue factoring: Now we need to factor 210. Again, it's an even number, so it's divisible by 2.
210 = 2 × 105
-
Keep going: Now we have 105. This is not divisible by 2, but it is divisible by 3 (1+0+5=6, which is divisible by 3).
105 = 3 × 35
-
Almost there: We're left with 35. This is not divisible by 2 or 3, but it is divisible by 5.
35 = 5 × 7
-
Prime factors identified: We have reached two prime numbers, 5 and 7. Neither of these can be factored further.
Therefore, the prime factorization of 420 is 2 × 2 × 3 × 5 × 7, which can be written more concisely as 2² × 3 × 5 × 7.
Visualizing Prime Factorization with a Factor Tree
A factor tree provides a visual representation of the factorization process:
420
/ \
2 210
/ \
2 105
/ \
3 35
/ \
5 7
This tree clearly shows how 420 is broken down into its prime factors. Each branch ends with a prime number.
Applications of Prime Factorization
Prime factorization isn't just an academic exercise; it has several practical applications:
-
Cryptography: Many modern encryption methods rely heavily on the difficulty of factoring very large numbers into their prime factors. The security of these systems depends on the computational intensity of finding the prime factors of extremely large composite numbers.
-
Computer Science: Prime factorization is crucial in algorithms related to number theory and cryptography within computer science. Efficient algorithms for prime factorization are constantly being researched and improved.
-
Simplifying Fractions: Finding the prime factors of the numerator and denominator of a fraction allows for simplification by canceling out common factors.
-
Least Common Multiple (LCM) and Greatest Common Divisor (GCD): Prime factorization simplifies calculating the LCM and GCD of two or more numbers, which is essential in various mathematical and scientific applications.
Beyond the Basics: Exploring Advanced Concepts
While the factor tree method is excellent for smaller numbers, more sophisticated algorithms exist for factoring larger numbers. These algorithms are vital for tackling the challenges posed by cryptography and other complex computational problems.
-
Trial Division: This is a straightforward method but becomes inefficient for large numbers.
-
Sieve of Eratosthenes: A more efficient method for finding all prime numbers up to a specified limit. It’s a fundamental tool in number theory.
-
Pollard's Rho Algorithm: A probabilistic algorithm suitable for finding small prime factors relatively quickly.
-
General Number Field Sieve (GNFS): The most efficient known algorithm for factoring very large numbers, used in breaking certain cryptographic systems. Understanding the complexities of GNFS requires advanced mathematical knowledge.
The Significance of the Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic guarantees that every composite number has a unique prime factorization. This uniqueness is critical because it provides a foundation for many other mathematical concepts and applications. It allows us to perform various calculations and manipulations in a consistent and predictable way. The uniqueness ensures that there's only one correct answer when finding the prime factors of any given number.
Expanding Your Understanding of Number Theory
Exploring prime numbers and their properties opens a fascinating realm of mathematical inquiry. Here are some areas to further explore:
-
Distribution of Primes: Investigating the patterns and distribution of prime numbers along the number line. The Prime Number Theorem provides an approximation of the number of primes less than a given number.
-
Twin Primes: Pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). The twin prime conjecture postulates that there are infinitely many twin prime pairs, a problem that remains unsolved.
-
Mersenne Primes: Prime numbers that are one less than a power of 2 (e.g., 7, 31, 127). Finding these primes is an active area of research, with the Great Internet Mersenne Prime Search (GIMPS) constantly pushing the boundaries.
-
Goldbach's Conjecture: This unsolved conjecture states that every even integer greater than 2 can be expressed as the sum of two primes.
Conclusion
Finding the prime factors of 420, while seemingly a simple task, serves as a gateway to understanding fundamental concepts in number theory. The process of prime factorization, as illustrated with the factor tree and discussed with various algorithms, is a cornerstone of mathematics with significant implications in cryptography, computer science, and other fields. The uniqueness guaranteed by the Fundamental Theorem of Arithmetic underpins much of our ability to work with numbers reliably and predictably. This exploration into the prime factors of 420, therefore, goes far beyond a simple mathematical calculation; it highlights the rich and enduring power of prime numbers in shaping our understanding of mathematics and its applications. Further exploration of related concepts will undoubtedly deepen your appreciation for the elegance and power of number theory.
Latest Posts
Latest Posts
-
Peasants And Workers Party Of India
Apr 03, 2025
-
Compressions And Rarefactions Are Characteristics Of
Apr 03, 2025
-
Explain The Process Of Making Yarn From Fibre Answer
Apr 03, 2025
-
Does Lemon Juice Dissolve In Water
Apr 03, 2025
-
The Process Of Photosynthesis Occurs In Organelles Called
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 420 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
