What Are The Prime Factorization Of 85
Juapaving
Mar 26, 2025 · 5 min read
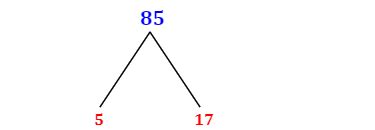
Table of Contents
What are the Prime Factorization of 85? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 85?" opens a door to a fascinating world of number theory. While the answer itself is straightforward, understanding the process and the underlying concepts of prime numbers and factorization is crucial for anyone interested in mathematics, computer science, or cryptography. This article will not only answer the question but delve deep into the methods, applications, and significance of prime factorization.
Understanding Prime Numbers
Before we tackle the factorization of 85, let's establish a solid foundation by defining prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
It's important to note that the definition of prime numbers forms the bedrock of many mathematical concepts. Their unique divisibility properties make them fundamental building blocks in number theory.
Distinguishing Prime Numbers from Composite Numbers
The opposite of a prime number is a composite number. A composite number is a natural number greater than 1 that is not prime – meaning it has divisors other than 1 and itself. For example, 4 (2 x 2), 6 (2 x 3), 9 (3 x 3), and 10 (2 x 5) are all composite numbers.
The distinction between prime and composite numbers is critical when performing factorization. Every composite number can be expressed uniquely as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic.
The Prime Factorization of 85
Now, let's address the main question: What is the prime factorization of 85? To find the prime factorization of a number, we systematically break it down into its prime components. There are several methods to achieve this.
Method 1: Factor Tree
One common method is using a factor tree. We start by finding any two factors of 85. A quick observation reveals that 85 is divisible by 5:
85
/ \
5 17
We see that 5 is a prime number. However, 17 is also a prime number. Therefore, the prime factorization of 85 is simply 5 x 17.
Method 2: Successive Division by Prime Numbers
Another approach involves dividing the number successively by prime numbers starting with the smallest prime number, 2. If the number is not divisible by 2, we move to the next prime number, 3, and so on.
- Check for divisibility by 2: 85 is not divisible by 2 (it's an odd number).
- Check for divisibility by 3: 85 is not divisible by 3 (the sum of its digits, 8 + 5 = 13, is not divisible by 3).
- Check for divisibility by 5: 85 is divisible by 5 (85 / 5 = 17).
- Check for divisibility of the quotient: The quotient is 17, which is a prime number.
This method also leads us to the prime factorization: 5 x 17.
The Significance of Prime Factorization
The seemingly simple process of prime factorization has far-reaching implications across various fields:
Cryptography
Prime factorization is the cornerstone of many modern encryption algorithms. The difficulty of factoring very large numbers into their prime components is the foundation of the security of systems like RSA, a widely used public-key cryptography system. The security relies on the fact that while multiplying two large prime numbers is computationally easy, factoring their product back into the original primes is extremely difficult.
Computer Science
Prime factorization plays a role in various algorithms and data structures used in computer science. For example, efficient algorithms for finding prime numbers are crucial for generating secure cryptographic keys and optimizing certain data structures.
Number Theory
Within number theory itself, prime factorization is a fundamental concept. It's used to prove various theorems and solve Diophantine equations (equations involving integers). The study of prime numbers and their distribution is a major area of research in number theory.
Advanced Concepts Related to Prime Factorization
While we've covered the basics, some more advanced concepts further illuminate the significance of prime factorization:
Unique Prime Factorization Theorem (Fundamental Theorem of Arithmetic)
This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This uniqueness is crucial in various mathematical applications.
Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization makes calculating the greatest common divisor (GCD) and least common multiple (LCM) of two or more numbers much easier. Finding the GCD and LCM is essential in various mathematical and computational contexts.
Distribution of Prime Numbers
The way prime numbers are distributed among integers is a fascinating topic. The Prime Number Theorem provides an approximation of the number of primes less than a given integer, highlighting the irregular yet predictable patterns in their distribution.
Prime Number Generation Algorithms
Various algorithms exist for generating prime numbers. These algorithms are essential in cryptography and other areas where large prime numbers are required. The Sieve of Eratosthenes is a classical algorithm for finding prime numbers up to a specified limit. More sophisticated algorithms are used for generating very large prime numbers required for robust cryptographic systems.
Conclusion: Beyond the Simple Answer
The prime factorization of 85, simply 5 x 17, is more than just a mathematical calculation. It's a gateway to understanding fundamental concepts in number theory, which have profound implications for computer science, cryptography, and numerous other fields. Understanding the methods for finding prime factorizations and appreciating their deeper significance is key to unlocking a deeper understanding of mathematics and its applications in the modern world. The simplicity of the answer belies the complex and fascinating world of prime numbers and their applications. This understanding allows us to not only solve simple factorization problems but also to appreciate the theoretical underpinnings that shape our digital world.
Latest Posts
Latest Posts
-
What Is The Lcm Of 7 5 And 3
Mar 29, 2025
-
How Long Do Silk Moths Live
Mar 29, 2025
-
Lcm Of 9 12 And 18
Mar 29, 2025
-
What Do You Call A Group Of Kangaroos
Mar 29, 2025
-
What Is The Square Root Of 3600
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Are The Prime Factorization Of 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
