What Are The Multiples Of 49
Juapaving
Apr 02, 2025 · 5 min read
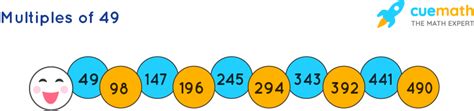
Table of Contents
What Are the Multiples of 49? A Deep Dive into Number Theory
The seemingly simple question, "What are the multiples of 49?" opens a door to a fascinating exploration within number theory. While the immediate answer involves straightforward multiplication, a deeper understanding reveals connections to prime factorization, divisibility rules, and even patterns within sequences. This article delves into the multifaceted nature of multiples of 49, providing a comprehensive guide for students, math enthusiasts, and anyone curious about the intricacies of numbers.
Understanding Multiples
Before we dive into the specifics of 49's multiples, let's establish a foundational understanding of what constitutes a multiple. A multiple of a number is the product of that number and any integer (whole number). For example, the multiples of 3 are 3, 6, 9, 12, 15, and so on, obtained by multiplying 3 by 1, 2, 3, 4, 5, respectively, and continuing infinitely in both positive and negative directions.
Finding Multiples of 49: The Basics
The simplest method for finding multiples of 49 is direct multiplication. We can systematically multiply 49 by each successive integer:
- 49 x 1 = 49
- 49 x 2 = 98
- 49 x 3 = 147
- 49 x 4 = 196
- 49 x 5 = 245
- 49 x 6 = 294
- 49 x 7 = 343
- 49 x 8 = 392
- 49 x 9 = 441
- 49 x 10 = 490
And so forth, continuing infinitely. This list represents the positive multiples of 49. To obtain negative multiples, we simply multiply 49 by negative integers (-1, -2, -3, etc.).
The Significance of Prime Factorization
The number 49 has a unique prime factorization: 7 x 7, or 7². Understanding this factorization provides deeper insights into its multiples. Every multiple of 49 will necessarily also be a multiple of 7, because it contains at least two factors of 7. This connection to its prime factors aids in identifying potential multiples and understanding divisibility rules.
Divisibility Rules and 49
While there isn't a widely known, simple divisibility rule specifically for 49 like there is for 2, 3, or 5, we can leverage the divisibility rule for 7 and the fact that 49 = 7². A number is divisible by 49 if it's divisible by 7 twice. This means a number must be divisible by 7, and the resulting quotient must also be divisible by 7.
Let's illustrate this with an example: Consider the number 2401.
- Divisibility by 7: 2401 / 7 = 343.
- Divisibility by 7 (again): 343 / 7 = 49.
Since both divisions result in whole numbers, 2401 is divisible by 49 (2401 = 49 x 49).
Patterns and Sequences in Multiples of 49
Observing the sequence of multiples of 49 reveals interesting patterns:
- The difference between consecutive multiples is always 49. This is a fundamental characteristic of any set of multiples of a given number.
- The units digits follow a repeating pattern: 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 9, 8, 7… This pattern repeats every ten multiples.
- The tens digits also exhibit a pattern, although it's less immediately obvious. Analyzing the tens and hundreds digits requires a more detailed mathematical investigation, but patterns certainly exist.
Applications and Real-World Examples
While the multiples of 49 might not seem immediately relevant to everyday life, understanding multiples is fundamental to various mathematical and practical applications:
- Measurement and Conversions: If you're working with units that involve multiples of 49 (though less common than multiples of 10 or other simpler numbers), understanding multiples is crucial for accurate calculations.
- Scheduling and Time Management: If a task repeats every 49 units of time (e.g., 49 days, 49 hours), knowing the multiples helps in scheduling and planning.
- Number Theory and Algebra: Multiples are fundamental concepts in number theory, forming the basis for many more advanced theorems and concepts.
- Computer Science: Multiples and divisibility play a role in algorithms and data structures.
Beyond the Basics: Exploring Advanced Concepts
The exploration of multiples of 49 can extend to more complex mathematical ideas:
- Arithmetic Sequences and Series: The sequence of multiples of 49 forms an arithmetic sequence, where the common difference is 49. We can use formulas to find the sum of a given number of terms in this sequence.
- Modular Arithmetic: Exploring the remainders when multiples of 49 are divided by other numbers leads into the fascinating world of modular arithmetic, a crucial aspect of cryptography and other areas of mathematics.
- Geometric Series (Related to 49² and higher powers): While not directly related to the multiples of 49 themselves, considering powers of 49 (49², 49³, etc.) introduces geometric sequences, another important concept in mathematics and its applications.
Conclusion: The Richness of Multiples of 49
The seemingly simple question of finding the multiples of 49 opens up a rich landscape within the study of numbers. From the basic act of multiplication to exploring prime factorization, divisibility rules, and the identification of patterns within sequences, the investigation offers a valuable glimpse into the intricacies and elegance of mathematics. The concepts explored here—multiples, prime factorization, divisibility, sequences, and patterns—are foundational to a deeper understanding of number theory and its many applications in various fields. Furthermore, understanding these principles fosters critical thinking and problem-solving skills crucial for success in various academic and professional endeavors. The journey into the world of multiples, even as seemingly straightforward as those of 49, is a testament to the unending depth and wonder inherent in the realm of mathematics.
Latest Posts
Latest Posts
-
How Many Sides Does An Octogon Have
Apr 03, 2025
-
The Pectoral Girdle Consists Of The
Apr 03, 2025
-
Find The Unit Vector In The Direction Of V
Apr 03, 2025
-
5 Letter Words Starting With Ho
Apr 03, 2025
-
Partial Fraction Decomposition Calculator Step By Step
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Are The Multiples Of 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
