What Are The Common Factors Of 28 And 36
Juapaving
Mar 31, 2025 · 5 min read
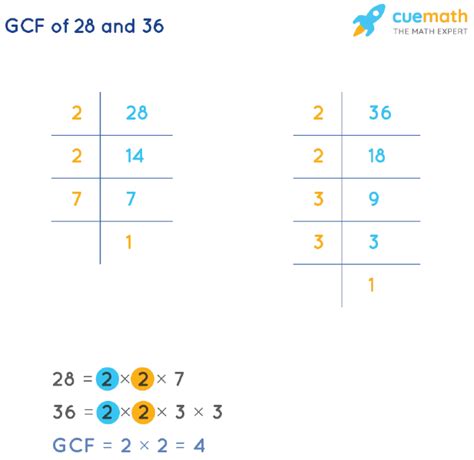
Table of Contents
What Are the Common Factors of 28 and 36? A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple arithmetic task, but it opens the door to a fascinating world of number theory. Understanding common factors is crucial in various mathematical fields, from simplifying fractions to solving complex algebraic equations. This comprehensive guide will explore the common factors of 28 and 36, explaining the process step-by-step and delving into the underlying mathematical concepts.
Understanding Factors and Common Factors
Before we dive into the specifics of 28 and 36, let's establish a firm understanding of the fundamental terms.
What is a Factor?
A factor of a number is a whole number that divides that number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 evenly.
What are Common Factors?
Common factors are numbers that are factors of two or more numbers. They are the numbers that divide each of the given numbers without leaving a remainder. For instance, the common factors of 12 and 18 are 1, 2, 3, and 6.
Finding the Common Factors of 28 and 36: A Step-by-Step Approach
Now, let's apply this knowledge to find the common factors of 28 and 36. We'll use two primary methods:
Method 1: Listing Factors
-
List the factors of 28: The factors of 28 are 1, 2, 4, 7, 14, and 28.
-
List the factors of 36: The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
-
Identify the common factors: By comparing the two lists, we can see that the common factors of 28 and 36 are 1, 2, and 4.
This method is straightforward for smaller numbers, but it can become cumbersome with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the numbers' structure.
-
Find the prime factorization of 28: 28 can be expressed as 2 x 2 x 7 (or 2² x 7).
-
Find the prime factorization of 36: 36 can be expressed as 2 x 2 x 3 x 3 (or 2² x 3²).
-
Identify common prime factors: Both 28 and 36 share two factors of 2 (2²).
-
Find the greatest common factor (GCF): The greatest common factor is the product of the common prime factors raised to the lowest power. In this case, the GCF is 2² = 4.
-
Find all common factors: The common factors are the factors of the GCF. Since the GCF is 4, the common factors are the factors of 4, which are 1, 2, and 4.
The Significance of the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the highest common factor (HCF), is the largest of the common factors. In the case of 28 and 36, the GCF is 4. The GCF plays a crucial role in various mathematical operations:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 28/36 can be simplified to 7/9 by dividing both the numerator and denominator by their GCF, 4.
-
Solving Equations: The GCF is often involved in solving algebraic equations and simplifying expressions.
-
Number Theory: The GCF is a fundamental concept in number theory, forming the basis for many advanced theorems and applications.
Beyond the Basics: Exploring Related Concepts
Understanding common factors opens the door to a deeper exploration of related number theory concepts.
Least Common Multiple (LCM)
The least common multiple (LCM) is the smallest number that is a multiple of two or more given numbers. While we've focused on common factors, the LCM is equally important and often used in conjunction with the GCF. For example, the LCM of 28 and 36 is 252.
The relationship between the GCF and LCM is given by the formula: GCF(a, b) x LCM(a, b) = a x b. This formula can be a helpful tool for finding either the GCF or LCM if one is already known.
Euclidean Algorithm
For larger numbers, the Euclidean algorithm is a highly efficient method for finding the GCF. This algorithm uses successive divisions to reduce the problem until the GCF is found. It's particularly useful when dealing with very large numbers where listing factors would be impractical.
Applications in Real-World Scenarios
The concepts of GCF and LCM have practical applications beyond the classroom:
-
Measurement and Division: When dealing with measurements (e.g., cutting fabric, dividing land), the GCF and LCM can help determine optimal sizes and divisions.
-
Scheduling: Finding the LCM is crucial in scheduling events that occur at regular intervals (e.g., buses arriving at a stop, machinery cycles).
-
Computer Science: GCF and LCM algorithms are fundamental in computer science, particularly in cryptography and data structures.
Conclusion: Mastering Common Factors
Understanding the common factors of numbers, particularly how to find the greatest common factor, is a fundamental skill in mathematics. This knowledge is not only essential for solving basic arithmetic problems but also forms the basis for understanding more advanced mathematical concepts. Whether you're simplifying fractions, solving equations, or exploring the fascinating world of number theory, mastering common factors will provide a strong foundation for your mathematical journey. By utilizing methods such as listing factors and prime factorization, and understanding the significance of the GCF and its relationship to the LCM, you can confidently tackle any problem involving common factors. The seemingly simple act of finding the common factors of 28 and 36 opens the door to a rich understanding of the underlying structure and beauty of numbers.
Latest Posts
Latest Posts
-
Is Rust Physical Or Chemical Change
Apr 01, 2025
-
Melting Of Wax Is A Physical Change
Apr 01, 2025
-
Why Do Fish And Frog Lay More Number Of Eggs
Apr 01, 2025
-
What Is 0 07 As A Percentage
Apr 01, 2025
-
Moment Of Inertia Of A Circle Formula
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Are The Common Factors Of 28 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
