What Are All Of The Factors Of 44
Juapaving
Mar 28, 2025 · 5 min read
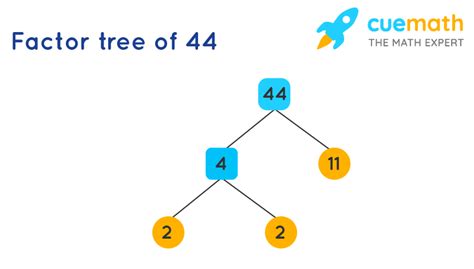
Table of Contents
What Are All of the Factors of 44? A Deep Dive into Factorization
Finding all the factors of a number might seem like a simple task, especially for smaller numbers like 44. However, understanding the process behind factorization opens up a world of mathematical concepts and applications. This comprehensive guide will not only identify all the factors of 44 but also explore the underlying principles of factorization, its importance in various fields, and some advanced considerations.
Understanding Factors and Factorization
Before diving into the specifics of 44, let's establish a clear understanding of what factors and factorization mean.
Factors: Factors of a number are whole numbers that divide evenly into that number without leaving a remainder. In other words, if 'a' is a factor of 'b', then b/a results in a whole number.
Factorization: Factorization, also known as prime factorization, is the process of breaking down a number into its prime factors. Prime factors are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This process is fundamental in many areas of mathematics and computer science.
Finding the Factors of 44: A Step-by-Step Approach
There are several ways to find all the factors of 44. Let's explore the most common methods:
Method 1: Systematic Division
This method involves systematically dividing 44 by each whole number, starting from 1, to identify which numbers divide evenly.
- Divide by 1: 44 / 1 = 44 (1 and 44 are factors)
- Divide by 2: 44 / 2 = 22 (2 and 22 are factors)
- Divide by 3: 44 / 3 = 14.666... (3 is not a factor)
- Divide by 4: 44 / 4 = 11 (4 and 11 are factors)
- Divide by 5: 44 / 5 = 8.8 (5 is not a factor)
- Divide by 6: 44 / 6 = 7.333... (6 is not a factor)
- Divide by 7: 44 / 7 = 6.285... (7 is not a factor)
- Divide by 8: 44 / 8 = 5.5 (8 is not a factor)
- Divide by 9: 44 / 9 = 4.888... (9 is not a factor)
- Divide by 10: 44 / 10 = 4.4 (10 is not a factor)
- Divide by 11: 44 / 11 = 4 (11 and 4 are already identified)
We stop here because the next number to try (12) is greater than the square root of 44 (approximately 6.63). Once we reach a factor larger than the square root, its corresponding pair will have already been found.
Therefore, the factors of 44 are 1, 2, 4, 11, 22, and 44.
Method 2: Prime Factorization
This method leverages the concept of prime numbers. We break down 44 into its prime factors and then use those factors to construct all possible combinations.
- Start with the smallest prime number: 44 is an even number, so it's divisible by 2. 44 / 2 = 22
- Continue with prime factors: 22 is also divisible by 2. 22 / 2 = 11
- Identify the prime factors: 11 is a prime number.
Therefore, the prime factorization of 44 is 2 x 2 x 11, or 2² x 11. Now, we can create all possible combinations of these prime factors to find all the factors:
- 2⁰ x 11⁰ = 1
- 2¹ x 11⁰ = 2
- 2² x 11⁰ = 4
- 2⁰ x 11¹ = 11
- 2¹ x 11¹ = 22
- 2² x 11¹ = 44
This again gives us the factors: 1, 2, 4, 11, 22, and 44.
Applications of Factorization
Factorization is not just a mathematical exercise; it has significant applications in various fields:
1. Cryptography
The security of many encryption methods relies on the difficulty of factoring large numbers into their prime factors. The RSA algorithm, widely used in secure online communication, is a prime example. The ability to quickly factor large numbers would compromise the security of these systems.
2. Computer Science
Factorization plays a crucial role in algorithms and data structures. Efficient factorization techniques are essential for tasks such as optimizing code, managing large datasets, and developing secure systems.
3. Number Theory
Factorization is a cornerstone of number theory, a branch of mathematics that deals with the properties of integers. It's used to prove theorems, solve complex equations, and explore the relationships between numbers.
4. Algebra
Factoring algebraic expressions is essential for simplifying equations, solving for unknown variables, and analyzing mathematical models. Many algebraic techniques rely on the principles of factorization.
Advanced Considerations: Beyond the Basics
While finding the factors of 44 is straightforward, the concept of factorization extends far beyond simple examples. Let's explore some more complex aspects:
1. Factoring Large Numbers
Factoring very large numbers is computationally intensive. Even with powerful computers, factoring extremely large numbers can take an incredibly long time. This difficulty is exploited in cryptography.
2. Unique Factorization Theorem (Fundamental Theorem of Arithmetic)
This fundamental theorem states that every integer greater than 1 can be represented as a unique product of prime numbers, disregarding the order of the factors. This uniqueness is crucial in many mathematical proofs and algorithms.
3. Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
The concept of factors is intimately related to finding the greatest common divisor (GCD) and least common multiple (LCM) of two or more numbers. The GCD is the largest number that divides both numbers evenly, while the LCM is the smallest number that is a multiple of both.
4. Modular Arithmetic
Modular arithmetic, which involves performing arithmetic operations within a specific modulus (remainder), often utilizes factorization to simplify calculations and solve congruence equations.
Conclusion: The Significance of Factorization
This detailed exploration of the factors of 44 has revealed not only the simple answer (1, 2, 4, 11, 22, 44) but also the significant implications of factorization in various fields. Understanding factorization is not just about finding the divisors of a number; it's about grasping a fundamental concept that underpins many advanced mathematical concepts and practical applications in computer science, cryptography, and beyond. The seemingly simple act of factoring opens up a rich and complex world of mathematical exploration.
Latest Posts
Latest Posts
-
Mass Of An Electron In Mev
Mar 31, 2025
-
From A Gas To A Liquid
Mar 31, 2025
-
How Many Feet Is 16 Meters
Mar 31, 2025
-
Examples Of Gas To A Liquid
Mar 31, 2025
-
Horizontal Cross Section Of A Cone
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Are All Of The Factors Of 44 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
