What Are All Factors Of 40
Juapaving
Mar 28, 2025 · 5 min read
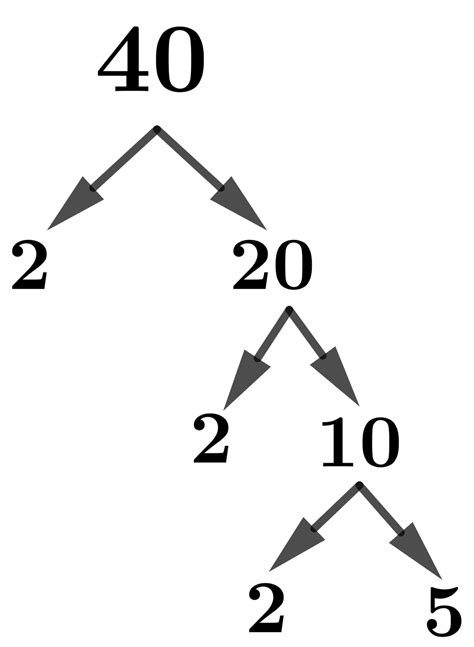
Table of Contents
What Are All the Factors of 40? A Deep Dive into Number Theory
Finding all the factors of a number might seem like a simple arithmetic task, but it opens a door to a fascinating world of number theory. Understanding factors is fundamental to many mathematical concepts, including prime factorization, greatest common divisors, and least common multiples. This article delves deep into finding all the factors of 40, exploring the methods involved and connecting them to broader mathematical principles.
Understanding Factors
Before we dive into the factors of 40, let's define what a factor is. A factor (or divisor) of a number is a whole number that divides the number evenly, leaving no remainder. In other words, if 'a' is a factor of 'b', then b/a is a whole number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Finding the Factors of 40: A Systematic Approach
There are several ways to find all the factors of 40. Let's explore a few methods:
Method 1: Trial Division
This is the most straightforward method. We systematically check each whole number from 1 up to the square root of 40 (approximately 6.32) to see if it divides 40 evenly. For each number that divides 40, we also find its corresponding pair.
- 1: 40/1 = 40. Therefore, 1 and 40 are factors.
- 2: 40/2 = 20. Therefore, 2 and 20 are factors.
- 4: 40/4 = 10. Therefore, 4 and 10 are factors.
- 5: 40/5 = 8. Therefore, 5 and 8 are factors.
- 6: 40/6 is not a whole number.
- We stop at 6 because the next whole number after 6 is greater than the square root of 40.
Therefore, the factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40.
Method 2: Prime Factorization
This method utilizes the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
-
Find the prime factorization of 40: 40 = 2 x 2 x 2 x 5 = 2³ x 5¹
-
Use the prime factorization to find all the factors: To find all the factors, we consider all possible combinations of the prime factors and their powers.
- Combinations of 2: 2⁰ (1), 2¹, 2², 2³ (8)
- Combinations of 5: 5⁰ (1), 5¹ (5)
Now, we combine these to find all factors:
- 1 (2⁰ x 5⁰)
- 2 (2¹ x 5⁰)
- 4 (2² x 5⁰)
- 8 (2³ x 5⁰)
- 5 (2⁰ x 5¹)
- 10 (2¹ x 5¹)
- 20 (2² x 5¹)
- 40 (2³ x 5¹)
This confirms that the factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40.
Connecting Factors to Other Mathematical Concepts
Understanding factors is crucial for various mathematical concepts:
1. Greatest Common Divisor (GCD)
The greatest common divisor (GCD) of two or more numbers is the largest number that divides all of them without leaving a remainder. For example, let's find the GCD of 40 and 60.
- Prime factorization of 40: 2³ x 5
- Prime factorization of 60: 2² x 3 x 5
The common prime factors are 2² and 5. Therefore, the GCD(40, 60) = 2² x 5 = 20.
2. Least Common Multiple (LCM)
The least common multiple (LCM) of two or more numbers is the smallest number that is a multiple of all of them. Let's find the LCM of 40 and 60.
- Prime factorization of 40: 2³ x 5
- Prime factorization of 60: 2² x 3 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization: 2³ x 3 x 5 = 120. Therefore, LCM(40, 60) = 120.
3. Perfect Numbers
A perfect number is a positive integer that is equal to the sum of its proper divisors (divisors excluding the number itself). 6 is a perfect number because its proper divisors (1, 2, 3) add up to 6. 40 is not a perfect number because the sum of its proper divisors (1+2+4+5+8+10+20) is 40, not 40.
4. Abundant and Deficient Numbers
-
Abundant numbers: These numbers are less than the sum of their proper divisors. 40 is an abundant number (1+2+4+5+8+10+20 = 50 > 40).
-
Deficient numbers: These numbers are greater than the sum of their proper divisors. For example, 16 is a deficient number (1+2+4+8 = 15 < 16).
Applications of Factors in Real-World Scenarios
While finding factors might seem like a purely mathematical exercise, it has practical applications in various fields:
-
Cryptography: Factorization plays a crucial role in modern cryptography, particularly in RSA encryption, which relies on the difficulty of factoring large numbers.
-
Scheduling and resource allocation: Finding the LCM is essential in scheduling tasks or allocating resources where events need to align periodically. For example, if two machines need maintenance every 40 days and 60 days, respectively, the LCM (120 days) determines when both machines will require maintenance simultaneously.
-
Geometry and measurements: Factors are used in determining possible dimensions for objects with specific areas or volumes. For instance, finding the possible dimensions of a rectangular plot with an area of 40 square meters.
-
Computer science: Factorization is used in various algorithms and data structures, such as finding the GCD for optimizing computations.
Conclusion
Finding all the factors of 40, while seemingly a simple task, offers a glimpse into the fascinating world of number theory. By understanding the methods involved and their connections to concepts like GCD, LCM, perfect numbers, and abundant/deficient numbers, we appreciate the broader significance of this fundamental mathematical operation. The applications of factors extend far beyond the classroom, impacting diverse fields such as cryptography, scheduling, and computer science. Mastering factor finding is a significant step toward a deeper understanding of the intricacies of numbers and their role in shaping our world.
Latest Posts
Latest Posts
-
Nouns That Start With A C
Mar 31, 2025
-
Which Are The Most Abundant Gases In The Atmosphere
Mar 31, 2025
-
What Are Three Examples Of A Chemical Change
Mar 31, 2025
-
What Is Prime Factors Of 24
Mar 31, 2025
-
Notes On Newtons Laws Of Motion
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Are All Factors Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
