Twin Prime Numbers From 1 To 100
Juapaving
Mar 31, 2025 · 6 min read
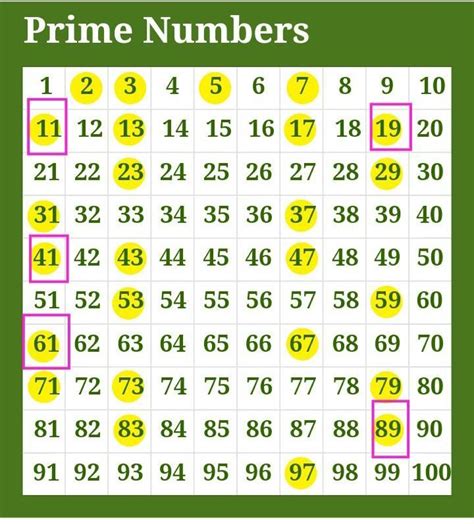
Table of Contents
Twin Prime Numbers from 1 to 100: A Deep Dive
Twin primes, a fascinating subset of prime numbers, ignite curiosity among mathematicians and number theory enthusiasts alike. This article delves into the world of twin primes, specifically examining those found within the range of 1 to 100. We'll explore their definition, properties, distribution, and the ongoing research surrounding this intriguing mathematical concept. We'll also touch upon the historical context and the significance of twin primes in the broader landscape of number theory.
Understanding Prime and Twin Prime Numbers
Before we embark on our journey into the world of twin primes from 1 to 100, let's establish a firm understanding of the fundamental concepts.
Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Prime numbers form the building blocks of all other natural numbers through factorization.
Twin Prime Numbers: Twin primes are pairs of prime numbers that differ by 2. For instance, (3, 5), (5, 7), (11, 13), and (17, 19) are all examples of twin prime pairs. The intriguing aspect of twin primes lies in their seemingly random distribution among the natural numbers. Despite their seemingly simple definition, their properties and distribution continue to be a subject of active mathematical research. The twin prime conjecture, one of the most famous unsolved problems in number theory, postulates that there are infinitely many twin prime pairs.
Identifying Twin Primes from 1 to 100
Let's systematically identify all the twin prime pairs within the range of 1 to 100. We can do this by listing all prime numbers in this range and then checking for pairs that differ by 2:
The prime numbers from 1 to 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Now, let's identify the twin prime pairs:
- (3, 5): The smallest twin prime pair.
- (5, 7): Another small and easily identifiable pair.
- (11, 13): A classic example frequently used in introductory number theory discussions.
- (17, 19): Yet another easily recognizable twin prime pair.
- (29, 31): These primes are relatively close together within the sequence.
- (41, 43): A pair situated in the mid-range of our set.
- (59, 61): Another example showcasing the seemingly sporadic nature of twin primes.
- (71, 73): This pair highlights the continued existence of twin primes even at larger values.
Therefore, there are eight twin prime pairs between 1 and 100.
The Distribution of Twin Primes: A Glimpse into the Infinite
The distribution of twin primes is a captivating area of study. While we've identified eight pairs from 1 to 100, the frequency of twin primes decreases as we move towards larger numbers. This doesn't necessarily mean that they stop; the twin prime conjecture suggests otherwise. However, finding larger twin prime pairs requires significantly more computational power.
The apparent irregularity in the distribution of twin primes is what makes them so intriguing. Unlike some number sequences with predictable patterns, twin primes seem to appear sporadically, adding to the mystery surrounding their properties. Their unpredictable nature poses significant challenges for mathematicians trying to develop formulas or algorithms that can accurately predict their occurrence.
The Brun's Constant
While the twin prime conjecture remains unproven, Brun's theorem provides a fascinating insight into the distribution of twin primes. Brun's theorem states that the sum of the reciprocals of all twin primes converges to a finite value, known as Brun's constant. This constant, approximately 1.90216, provides a quantitative measure of how "sparse" twin primes are within the natural numbers. The fact that the sum converges suggests that twin primes become increasingly rare as we move towards larger numbers, even if they extend infinitely.
The Significance of Twin Primes in Number Theory
The study of twin primes holds significant importance in number theory for several reasons:
-
Unsolved Conjecture: The twin prime conjecture, proposing an infinite number of twin primes, remains one of the most significant unsolved problems in mathematics. Its resolution would have profound implications for our understanding of prime number distribution and related fields.
-
Connection to the Riemann Hypothesis: The twin prime conjecture is deeply intertwined with the Riemann Hypothesis, another unsolved problem of paramount importance in number theory. Advances in understanding one could potentially lead to breakthroughs in the other.
-
Testing Number-Theoretic Concepts: Twin primes provide an excellent testing ground for various number-theoretic concepts and algorithms. Studying their distribution and properties helps refine our tools and approaches to tackling more complex problems.
-
Algorithmic Challenges: Finding large twin primes presents significant computational challenges, pushing the boundaries of algorithmic efficiency and computational power. Research in this area contributes to advancements in computer science and algorithm design.
Beyond the Basics: Further Explorations
The world of twin primes extends far beyond the range of 1 to 100. Here are some further areas of exploration:
-
Larger Twin Primes: The search for increasingly larger twin primes is an ongoing pursuit. Finding these primes requires sophisticated algorithms and substantial computational resources. The largest known twin primes are constantly being updated as computational power improves.
-
Higher-Order Primes: Similar to twin primes, there's the concept of higher-order prime constellations, such as triplet primes (primes that differ by 2, such as 3,5,7 but is not considered a twin prime) or cousin primes (primes that differ by 4, such as 3 and 7, 7 and 11). These further extend the study of prime number distributions.
-
Prime Gaps: The distance between consecutive primes is known as a prime gap. The study of prime gaps is closely related to the study of twin primes, as twin primes represent prime gaps of size 2.
Conclusion: The Enduring Mystery of Twin Primes
The study of twin primes, even within the seemingly limited range of 1 to 100, provides a compelling glimpse into the intricate world of prime numbers. The eight pairs we've identified represent just a small fraction of the potentially infinite number of twin primes that exist. The enduring mystery surrounding their distribution, coupled with their connection to some of the most significant unsolved problems in mathematics, makes them a subject of continued fascination and active research. As computational power advances and mathematical techniques evolve, we can anticipate further progress in unraveling the secrets held within these captivating number pairs. The quest to understand twin primes is a testament to the enduring power of human curiosity and our relentless pursuit of knowledge within the fascinating realm of mathematics.
Latest Posts
Latest Posts
-
Fractions Name The Same Part Of The Same Whole
Apr 02, 2025
-
Calcium Hydroxide Is Acid Or Base
Apr 02, 2025
-
What Is The Chemical Formula Of Protein
Apr 02, 2025
-
What Is The National Animal Of Australia
Apr 02, 2025
-
Three Or More Points That Lie In The Same Line
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Twin Prime Numbers From 1 To 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
