Three Or More Points That Lie In The Same Line
Juapaving
Apr 02, 2025 · 6 min read
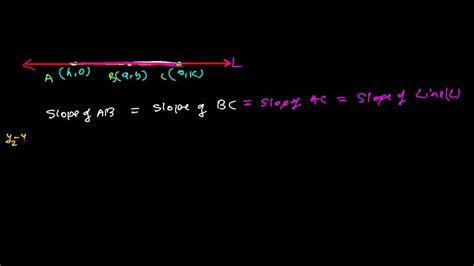
Table of Contents
Collinearity: When Three or More Points Align
Collinearity, in the simplest terms, describes the property of three or more points lying on the same straight line. This seemingly basic geometric concept plays a significant role in various fields, from computer graphics and spatial analysis to linear algebra and projective geometry. Understanding collinearity requires delving into its definition, identifying methods for determining it, and exploring its applications in different contexts. This article will comprehensively cover these aspects, providing a solid foundation for anyone interested in this fundamental geometric principle.
Defining Collinearity: The Straight Line Connection
The core idea behind collinearity is straightforward: points are collinear if they all lie on a single straight line. No matter how many points we are considering, if a single line can be drawn to pass through all of them without deviation, then those points are collinear. This seemingly simple definition, however, opens up several avenues for investigation and application.
Visualizing Collinearity
Imagine three points, A, B, and C, scattered on a piece of paper. If you can draw a perfectly straight line that passes through all three points without needing to alter its course, then points A, B, and C are collinear. However, if the line connecting A and B does not also pass through C, then they are not collinear. The same principle applies to four, five, or any number of points. All must lie on the same straight line for collinearity to hold.
Differentiating Collinearity from Other Geometric Concepts
It's crucial to distinguish collinearity from related but distinct geometric concepts:
- Coplanarity: While collinearity focuses on points lying on the same line, coplanarity addresses points residing on the same plane (a flat two-dimensional surface). All collinear points are coplanar, but not all coplanar points are collinear.
- Concurrency: This concept refers to lines intersecting at a single point. Although related to the arrangement of points and lines, it's a different geometric property than collinearity.
Methods for Determining Collinearity
Several methods exist for determining whether a set of points is collinear. The most common involve using the concept of slope and the equation of a line.
1. Using the Slope Formula: The Foundation of Collinearity Tests
The slope of a line represents the steepness of the line and is calculated as the change in the y-coordinate divided by the change in the x-coordinate between any two points on that line. If three or more points are collinear, the slope between any pair of points will be the same.
The Formula: The slope (m) between points (x₁, y₁) and (x₂, y₂) is given by: m = (y₂ - y₁) / (x₂ - x₁)
Applying the Slope Test: To test for collinearity using the slope method:
- Calculate the slope between the first two points.
- Calculate the slope between the second and third points.
- Calculate the slope between the first and third points (and any subsequent points if there are more than three).
- Compare the slopes: If all slopes are equal, the points are collinear. If even one slope differs, the points are not collinear.
Important Considerations: This method fails if the line is vertical (x₂ - x₁ = 0), resulting in an undefined slope. In such cases, alternative methods are necessary.
2. Using the Equation of a Line: A More Robust Approach
The equation of a line, typically expressed in the form y = mx + c (where m is the slope and c is the y-intercept), provides a more robust approach to determining collinearity, particularly when dealing with vertical lines.
Applying the Line Equation Method:
- Select any two points: Use these to find the equation of the line passing through them.
- Substitute the coordinates of the remaining points: Substitute the x-coordinate of each remaining point into the line equation. If the resulting y-value matches the point's actual y-coordinate, the point lies on the line.
- Repeat: Repeat Step 2 for all remaining points. If all points satisfy the line equation, they are collinear.
This method elegantly handles vertical lines since their equations are of the form x = constant.
3. Determinant Method: A Powerful Technique for Multiple Points
For a more efficient method, especially when dealing with multiple points in higher dimensions, the determinant method utilizes the concept of matrices and determinants.
Applying the Determinant Method:
For three points (x₁, y₁), (x₂, y₂), and (x₃, y₃), construct the following matrix:
| x₁ y₁ 1 |
| x₂ y₂ 1 |
| x₃ y₃ 1 |
Calculate the determinant of this matrix. If the determinant is zero, the points are collinear. This method extends easily to higher dimensions. For example, in 3D space, you would add a z-coordinate and a fourth column of 1s to the matrix.
Applications of Collinearity
The concept of collinearity isn't just a theoretical exercise; it finds practical application in numerous fields:
1. Computer Graphics and Image Processing
Collinearity plays a vital role in computer graphics and image processing. Algorithms for detecting lines and edges in images often rely on identifying sets of collinear pixels. This is essential for tasks like image segmentation, object recognition, and feature extraction.
2. Geographic Information Systems (GIS) and Spatial Analysis
In GIS, collinearity is crucial for spatial analysis. Identifying collinear points helps in understanding spatial relationships and patterns, such as the alignment of buildings along a street or the distribution of points along a geological fault line. This aids in tasks like route planning, urban planning, and environmental modeling.
3. Linear Algebra and Geometry
In linear algebra, collinearity is intrinsically linked to concepts like linear dependence and vector spaces. Collinear points represent linearly dependent vectors, implying that one vector can be expressed as a linear combination of the others. This understanding is fundamental to solving systems of linear equations and performing various geometric transformations.
4. Surveying and Mapping
In surveying and mapping, collinearity is essential for accurate land measurement and map creation. Techniques like triangulation rely on the precise measurement of angles and distances to determine the positions of points, and the assumption of collinearity between specific points is often made.
5. Physics and Engineering
In various physics and engineering applications, collinearity plays a role in analyzing forces, vectors, and trajectories. For instance, determining if forces acting on an object are collinear is crucial in assessing stability and equilibrium.
Beyond the Basics: Extending Collinearity
The concept of collinearity can be extended in several ways:
- Higher Dimensions: Collinearity isn't restricted to two-dimensional space. The principles extend seamlessly to three-dimensional (3D) space and even higher dimensions, albeit with more complex calculations.
- Statistical Collinearity: In statistics, collinearity (or multicollinearity) refers to a situation where predictor variables in a regression model are highly correlated. This can impact the accuracy and stability of the regression model.
- Projective Geometry: Projective geometry provides a powerful framework for studying collinearity, particularly in the context of transformations and perspectives.
Conclusion: The Enduring Significance of Collinearity
Collinearity, despite its apparent simplicity, is a fundamental geometric concept with far-reaching implications across multiple disciplines. Understanding the various methods for determining collinearity and appreciating its applications provides valuable insight into the underlying structure of geometric relationships and their practical relevance in diverse fields. From image analysis to spatial analysis and beyond, the ability to recognize and utilize collinearity remains a powerful tool for understanding and interpreting the world around us. The methods outlined here—slope calculations, line equations, and determinant methods—provide a comprehensive toolkit for investigating and applying this crucial geometric principle.
Latest Posts
Latest Posts
-
Least Common Multiple For 3 4 5
Apr 03, 2025
-
Drawing Of Law Of Conservation Of Mass
Apr 03, 2025
-
A Homogeneous Mixture Is Also Called A
Apr 03, 2025
-
A Substance Formed During A Chemical Reaction
Apr 03, 2025
-
Give The Major Product Of The Following Reaction
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Three Or More Points That Lie In The Same Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
