The Si Unit Of Force Is
Juapaving
Mar 29, 2025 · 6 min read
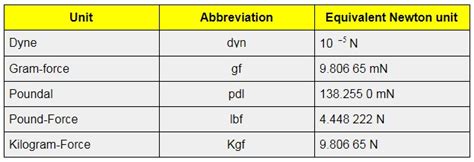
Table of Contents
The SI Unit of Force Is: A Deep Dive into Newtons
The SI unit of force is the newton, symbolized by N. Understanding the newton, its origins, applications, and relationship to other units is crucial in various scientific fields, from classical mechanics to advanced physics. This comprehensive guide will delve into the intricacies of the newton, exploring its definition, practical applications, and connections to other fundamental SI units.
Defining the Newton: More Than Just a Unit
The newton isn't just a randomly chosen unit; it's meticulously defined based on fundamental physical principles. Specifically, one newton is defined as the amount of force required to accelerate a mass of one kilogram at a rate of one meter per second squared. This definition neatly encapsulates Newton's second law of motion, a cornerstone of classical mechanics: F = ma, where:
- F represents force (measured in newtons)
- m represents mass (measured in kilograms)
- a represents acceleration (measured in meters per second squared)
This equation highlights the inherent connection between force, mass, and acceleration. A larger force will result in a greater acceleration for a given mass, and a larger mass will require a greater force to achieve the same acceleration. The simplicity and elegance of this definition make the newton a fundamental and universally understood unit of force.
The Significance of the Kilogram and Meter
The definition of the newton is inextricably linked to the kilogram (kg) and the meter (m), two other fundamental SI units. The kilogram represents the base unit of mass, while the meter represents the base unit of length. The stability and precision of these base units are crucial for maintaining the accuracy and consistency of the newton. Recent redefinitions of the kilogram and meter, based on fundamental physical constants, have further enhanced the accuracy and reliability of the newton.
Beyond the Basic Definition: Exploring Different Perspectives
While F = ma provides a concise definition, understanding the newton requires exploring its implications from various perspectives. Consider these points:
-
Weight vs. Mass: Often confused, weight and mass are distinct concepts. Mass is an intrinsic property of an object, representing the amount of matter it contains. Weight, on the other hand, is the force exerted on an object due to gravity. The weight of an object (in newtons) is calculated as W = mg, where g is the acceleration due to gravity (approximately 9.81 m/s² on Earth). This clarifies that an object's weight can vary depending on the gravitational field strength, while its mass remains constant.
-
Force as a Vector Quantity: The newton, like many other physical quantities, is a vector quantity. This means it possesses both magnitude (the numerical value of the force) and direction. Specifying only the magnitude of a force is insufficient; you must also specify its direction to fully describe it. This directional aspect is crucial in analyzing complex systems involving multiple forces.
-
Everyday Applications: The newton is not just a theoretical concept; it finds practical applications in countless everyday scenarios. From the force exerted when pushing a shopping cart to the force required to lift a weight, newtons are constantly at play. Understanding the magnitude of these forces can be beneficial in various activities, from engineering design to athletic performance analysis.
The Newton in Different Contexts: A Multifaceted Unit
The versatility of the newton is evident in its applications across various scientific and engineering disciplines. Here are a few examples:
1. Classical Mechanics
Newton's laws of motion form the backbone of classical mechanics, and the newton plays a central role in describing and analyzing motion, forces, and energy. Calculations involving forces, momentum, work, and energy invariably involve the newton. For instance, calculating the force required to accelerate a vehicle, the tension in a cable, or the impact force during a collision all require employing newtons.
2. Engineering
Engineers extensively utilize the newton in structural analysis, design, and material science. Determining the strength of materials, the load-bearing capacity of structures, and the stability of mechanical systems all rely on precise calculations involving forces measured in newtons. Civil engineers use newtons to analyze stresses and strains in bridges, buildings, and other structures. Mechanical engineers use it for designing engines, machines, and other mechanical systems.
3. Physics Beyond Classical Mechanics
While central to classical mechanics, the newton remains relevant in more advanced physics concepts. For instance, in electromagnetism, the force between charged particles (Coulomb's law) is expressed in newtons. Even in relativity, although the framework is different, forces still play a crucial role, and the newton retains its place as the fundamental unit.
4. Everyday Life
Beyond formal scientific and engineering contexts, we encounter newtons in our everyday lives, albeit implicitly. The force we apply when opening a door, the weight we lift, and the forces involved in simple actions are all expressed, albeit not explicitly, in newtons. Understanding the concept of force in newtons can help us better understand the physical world around us.
Conversions and Relationships with Other Units
The newton is not an isolated unit; it has well-defined relationships with other units of measurement. Understanding these conversions is essential for seamless transitions between different unit systems.
Relationship to Dynes
Before the widespread adoption of the SI system, the dyne was frequently used as a unit of force. One dyne is defined as the force required to accelerate a mass of one gram at a rate of one centimeter per second squared. The conversion factor is straightforward: 1 N = 10<sup>5</sup> dynes.
Relationship to Pounds-force
In the imperial system, the pound-force (lbf) is used as a unit of force. The conversion factor between newtons and pounds-force is approximately 1 N ≈ 0.2248 lbf, or equivalently, 1 lbf ≈ 4.448 N.
Relationship to other SI Units
The newton's relationship with other SI units is directly linked to its definition (F = ma). By manipulating this equation, we can derive relationships between force, mass, acceleration, and other related quantities such as momentum and energy. For instance, the unit of momentum (kg⋅m/s) can be expressed as N⋅s (newton-seconds), highlighting the connection between force and momentum.
Conclusion: The Enduring Importance of the Newton
The newton, as the SI unit of force, stands as a testament to the elegance and practicality of the International System of Units. Its clear definition, rooted in fundamental physical principles, ensures its widespread acceptance and application across various scientific and engineering disciplines. Understanding the newton goes beyond simply knowing its value; it's about grasping the underlying concepts of force, mass, acceleration, and their interplay in shaping our physical world. From the simplest everyday interactions to the most complex scientific calculations, the newton remains an indispensable tool for understanding and quantifying the forces that govern our universe. Its enduring relevance underscores its importance as a cornerstone of modern physics and engineering. Further exploration of its applications and connections to other units will only deepen your understanding of this vital unit of measurement.
Latest Posts
Latest Posts
-
Write The Prime Factorization Of 66
Mar 31, 2025
-
What Is 3 20 As A Percent
Mar 31, 2025
-
How Many Inches Are In 44 Feet
Mar 31, 2025
-
What Is 4 Kg Into Grams
Mar 31, 2025
-
What Is The Least Common Multiple Of 15 And 12
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about The Si Unit Of Force Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
