What Is 3/20 As A Percent
Juapaving
Mar 31, 2025 · 5 min read
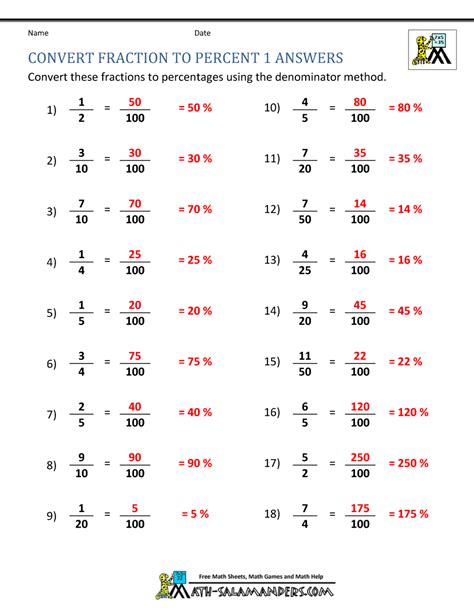
Table of Contents
What is 3/20 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields, from everyday finances to complex scientific calculations. This comprehensive guide delves into the process of converting the fraction 3/20 into a percentage, providing a step-by-step explanation, practical examples, and exploring related concepts to solidify your understanding.
Understanding Fractions and Percentages
Before we dive into the conversion, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 3/20, 3 is the numerator and 20 is the denominator.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of 100." Percentages are commonly used to represent proportions, rates, and changes.
Converting 3/20 to a Percentage: The Step-by-Step Method
There are two primary methods for converting a fraction to a percentage:
Method 1: Converting the Fraction to a Decimal First
This method involves two steps:
-
Divide the numerator by the denominator: Divide 3 by 20. This gives you 0.15.
-
Multiply the decimal by 100: Multiply 0.15 by 100. This gives you 15.
-
Add the percentage symbol: Add the "%" symbol to indicate that the result is a percentage.
Therefore, 3/20 is equal to 15%.
Method 2: Direct Conversion Using Equivalent Fractions
This method leverages the definition of a percentage as a fraction out of 100.
-
Find an equivalent fraction with a denominator of 100: To convert 3/20 to a percentage, we need to find an equivalent fraction where the denominator is 100. We can achieve this by multiplying both the numerator and the denominator by 5:
(3 * 5) / (20 * 5) = 15/100
-
Express the fraction as a percentage: Since the denominator is now 100, the numerator directly represents the percentage. Therefore, 15/100 is equal to 15%.
Both methods yield the same result: 3/20 is equivalent to 15%. Choosing the method that feels more intuitive to you is key to mastering this conversion.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, tax rates, and profit margins often involves converting fractions to percentages. For example, a 3/20 discount on a product means a 15% discount.
-
Statistics: Expressing data in percentages helps in visualizing and interpreting statistical information more effectively. For example, if 3 out of 20 students passed an exam, it means 15% of the students passed.
-
Science: Scientists often use percentages to represent concentrations, error margins, and experimental results.
-
Everyday Life: We encounter percentages regularly in everyday life, from calculating tips in restaurants to understanding sales and discounts in stores.
Expanding on Percentage Concepts: Understanding Percentage Increase and Decrease
Beyond simple conversion, understanding how percentages relate to increase and decrease is equally important.
Let's say you had 20 apples, and you received 3 more. The increase in your apple count can be expressed as a percentage.
-
Calculate the increase: 3 apples
-
Calculate the percentage increase: (Increase/Original Amount) * 100 = (3/20) * 100 = 15%
Therefore, you experienced a 15% increase in your apple count.
Conversely, if you started with 20 apples and ate 3, the decrease would be calculated as:
-
Calculate the decrease: 3 apples
-
Calculate the percentage decrease: (Decrease/Original Amount) * 100 = (3/20) * 100 = 15%
This represents a 15% decrease in your apple count.
Advanced Applications and Related Concepts
The foundation of understanding fractions and percentages extends to more advanced mathematical concepts:
-
Ratio and Proportion: Percentages are closely related to ratios and proportions. A ratio is a comparison of two quantities, and a proportion is a statement that two ratios are equal. Understanding these relationships allows for solving more complex problems involving percentages.
-
Compound Interest: Calculating compound interest involves repeated applications of percentage calculations, demonstrating the power of compounding over time.
-
Probability: Probabilities are often expressed as percentages, representing the likelihood of an event occurring.
-
Data Analysis: In data analysis, percentages are essential for summarizing, interpreting, and visualizing data effectively. For instance, calculating the percentage of respondents who chose a particular option in a survey.
Troubleshooting Common Mistakes
While the conversion of 3/20 to 15% is straightforward, several common mistakes can occur:
-
Incorrect division: Ensuring accurate division of the numerator by the denominator is crucial. A minor error in this step will lead to an incorrect percentage.
-
Forgetting to multiply by 100: Multiplying the resulting decimal by 100 is essential to express the fraction as a percentage. Omitting this step will result in a decimal value, not a percentage.
-
Incorrect interpretation of percentage increase/decrease: Understanding the context and using the correct formula for percentage increase or decrease is vital for accurate calculations.
Conclusion: Mastering Fraction-to-Percentage Conversion
Converting fractions to percentages is a versatile mathematical skill with applications across numerous domains. By understanding the underlying principles and practicing the conversion methods, you will enhance your mathematical proficiency and your ability to solve real-world problems involving proportions and percentages. Remember to always double-check your calculations to avoid common errors, and practice regularly to build confidence and fluency. The ability to confidently perform these conversions opens doors to a deeper understanding of mathematical concepts and their practical applications in various aspects of life. This knowledge is essential for navigating the numerical world effectively, from managing personal finances to interpreting data in professional settings.
Latest Posts
Latest Posts
-
What Shape Has 12 Edges 8 Vertices And 6 Faces
Apr 02, 2025
-
Different Ways To Write A Number
Apr 02, 2025
-
Least Common Multiple Of 8 And 4
Apr 02, 2025
-
How Many Neutrons Are In Potassium
Apr 02, 2025
-
Relation Between Linear And Angular Acceleration
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
