Surface Area Of Sphere And Hemisphere
Juapaving
Apr 05, 2025 · 5 min read
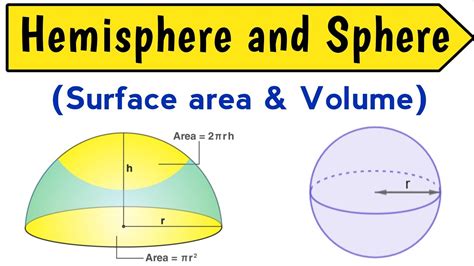
Table of Contents
Delving Deep into the Surface Area of Spheres and Hemispheres
The surface area of a sphere and a hemisphere are fundamental concepts in geometry with widespread applications in various fields, from engineering and architecture to physics and astronomy. Understanding how to calculate these areas is crucial for solving numerous real-world problems. This comprehensive guide will explore the formulas, derivations, and practical applications of these geometric calculations. We'll also delve into some advanced concepts and problem-solving strategies.
Understanding the Sphere
A sphere is a perfectly round three-dimensional object. Every point on its surface is equidistant from its center. This equidistant property is key to understanding its surface area calculation. The distance from the center to any point on the surface is called the radius (denoted as 'r'). The sphere’s surface area is the total area encompassing its three-dimensional form.
Deriving the Formula for the Surface Area of a Sphere
The derivation of the formula for the surface area of a sphere often involves calculus, specifically integration. However, we can visualize the concept more intuitively. Imagine slicing the sphere into many infinitesimally small strips. Each strip can be approximated as a thin, cylindrical band. The area of each band is proportional to the circumference of the circle at that latitude and the height of the band. Summing the areas of all these bands gives the total surface area. This process, when formalized using calculus, leads to the well-known formula:
Surface Area of a Sphere = 4πr²
where:
- r represents the radius of the sphere.
- π (pi) is a mathematical constant, approximately equal to 3.14159.
Understanding the Significance of 4π
The constant '4π' in the formula is not arbitrary. It represents the relationship between the sphere's volume and its surface area. This factor highlights the sphere's unique geometric properties and its efficiency in enclosing a volume.
The Hemisphere: Half the Sphere
A hemisphere is simply half of a sphere. It is created by slicing a sphere in half through its center. This results in a curved surface and a flat circular base. Understanding the surface area of a hemisphere involves calculating the curved surface area and the area of the circular base.
Calculating the Surface Area of a Hemisphere
To calculate the surface area of a hemisphere, we need to consider two components:
-
Curved Surface Area: This is half the surface area of the entire sphere. Therefore, the curved surface area of a hemisphere is: (1/2) * 4πr² = 2πr²
-
Area of the Circular Base: The base of the hemisphere is a circle with radius 'r'. The area of this circle is: πr²
Therefore, the total surface area of a hemisphere is the sum of its curved surface area and the area of its circular base:
Total Surface Area of a Hemisphere = 2πr² + πr² = 3πr²
Applications of Sphere and Hemisphere Surface Area Calculations
The formulas for the surface area of spheres and hemispheres have numerous applications across various disciplines:
1. Engineering and Architecture:
-
Designing Spherical Tanks: Calculating the surface area of spherical tanks is crucial for determining the amount of material needed for construction and for applying protective coatings.
-
Estimating Paint or Coating Requirements: In construction and architectural projects, determining the surface area of spherical or hemispherical domes or other structures is essential for accurate material estimations.
-
Aerospace Engineering: Calculating the surface area of spacecraft components or satellites is vital for thermal management and aerodynamic design.
2. Physics and Astronomy:
-
Calculating Gravitational Fields: The surface area of a sphere plays a critical role in understanding gravitational fields and their interactions with objects.
-
Modeling Celestial Bodies: Astronomers use the surface area of spheres and hemispheres to model planets, stars, and other celestial objects. This helps in calculating various parameters like luminosity and radiative energy.
-
Nuclear Physics: In nuclear physics, the surface area of a nucleus influences certain nuclear reactions and properties.
3. Medicine and Biology:
-
Modeling Cells and Biological Structures: Many biological structures, such as cells and certain organs, can be approximated as spheres or hemispheres, allowing for surface area calculations to understand their properties and interactions.
-
Drug Delivery Systems: Designing efficient drug delivery systems involves considering the surface area of nanoparticles or microspheres for optimal absorption and distribution within the body.
4. Meteorology:
- Estimating Rainfall: In meteorology, surface area calculations help to understand rainfall distribution and its impact on the Earth's surface.
Solving Problems Involving Surface Area: Examples
Let's work through a few examples to illustrate the practical application of these formulas:
Example 1: A spherical balloon has a radius of 10 cm. Calculate its surface area.
Using the formula: Surface Area = 4πr² = 4π(10 cm)² = 400π cm² ≈ 1256.64 cm²
Example 2: A hemispherical dome has a radius of 5 meters. Calculate its total surface area.
Using the formula: Total Surface Area = 3πr² = 3π(5 m)² = 75π m² ≈ 235.62 m²
Example 3: A spherical tank with a radius of 2 meters needs to be painted. If one liter of paint covers 10 square meters, how many liters of paint are needed?
First, calculate the surface area: Surface Area = 4π(2 m)² = 16π m² ≈ 50.27 m²
Then, divide the total surface area by the coverage per liter: 50.27 m² / 10 m²/liter ≈ 5.03 liters. Therefore, approximately 5.03 liters of paint are needed.
Advanced Concepts and Considerations
-
Surface Area of Irregular Shapes: While the formulas above apply to perfect spheres and hemispheres, many real-world objects have irregular shapes. In such cases, numerical methods or approximations may be needed to estimate the surface area. Techniques like triangulation and surface integration are commonly employed.
-
Units of Measurement: Always ensure consistency in units of measurement throughout your calculations. If the radius is given in centimeters, the surface area will be in square centimeters.
-
Dimensional Analysis: Dimensional analysis is a powerful tool to verify the correctness of your calculations. The units of the final answer should be consistent with the units of the input parameters.
Conclusion
The surface area of spheres and hemispheres is a fundamental concept with vast applications. Understanding the derivation and application of the formulas is crucial for solving diverse problems in engineering, physics, biology, and other fields. This guide has provided a comprehensive overview of these calculations, including examples and considerations for more complex scenarios. Mastering these calculations will enhance your problem-solving skills and provide a solid foundation for more advanced studies in mathematics and science. Remember to practice regularly to solidify your understanding and to apply these concepts creatively to new and challenging problems.
Latest Posts
Latest Posts
-
What Is The Si Unit Of Weight
Apr 05, 2025
-
A Particle Executes Simple Harmonic Motion
Apr 05, 2025
-
2 9 As A Decimal And Percent
Apr 05, 2025
-
Force Is A Scalar Or Vector Quantity
Apr 05, 2025
-
Are Diagonals Perpendicular In A Parallelogram
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Surface Area Of Sphere And Hemisphere . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
