Are Diagonals Perpendicular In A Parallelogram
Juapaving
Apr 05, 2025 · 5 min read
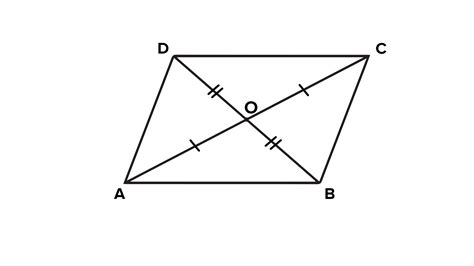
Table of Contents
Are Diagonals Perpendicular in a Parallelogram? Exploring the Geometry of Parallelograms
The question of whether diagonals are perpendicular in a parallelogram is a fundamental concept in geometry. While not true for all parallelograms, it is true for a specific type of parallelogram: the rhombus (and its special case, the square). Understanding this distinction is crucial for mastering geometric principles and problem-solving. This comprehensive guide will delve into the properties of parallelograms, focusing specifically on the relationship between their diagonals and perpendicularity. We'll explore various approaches to proving (or disproving) this relationship, solidify your understanding with examples, and provide you with a solid foundation for tackling more complex geometric problems.
Understanding Parallelograms: A Foundation
Before we tackle the central question, let's establish a strong understanding of parallelograms. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel. This seemingly simple definition leads to several important properties:
- Opposite sides are equal in length: This means that if we label the vertices of the parallelogram ABCD, then AB = CD and BC = AD.
- Opposite angles are equal: ∠A = ∠C and ∠B = ∠D.
- Consecutive angles are supplementary: This means that their sum equals 180 degrees. For example, ∠A + ∠B = 180°.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at a point called the midpoint. Each diagonal is divided into two equal segments by this intersection.
When are Diagonals Perpendicular? The Case of the Rhombus
While the diagonals of a general parallelogram bisect each other, they are not necessarily perpendicular. The exception to this is the rhombus. A rhombus is a parallelogram with all four sides equal in length. This additional constraint introduces perpendicularity between the diagonals.
Theorem: The diagonals of a rhombus are perpendicular bisectors of each other.
Proof:
Let's consider a rhombus ABCD. We know that AB = BC = CD = DA. Let's denote the intersection point of the diagonals AC and BD as O.
-
Diagonals bisect each other: This is a property of all parallelograms, as stated previously. Therefore, AO = OC and BO = OD.
-
Consider triangles ΔAOB and ΔBOC: Since AB = BC (sides of the rhombus) and AO = OC (diagonals bisect each other), and OB is a common side, we can use the SSS (Side-Side-Side) congruence postulate to conclude that ΔAOB ≅ ΔBOC.
-
Angles are equal: Due to the congruence of triangles, ∠AOB = ∠BOC. Since ∠AOB and ∠BOC are adjacent angles on a straight line (AC), their sum is 180°. Therefore, ∠AOB = ∠BOC = 90°.
-
Perpendicularity: This proves that the diagonals AC and BD intersect at a 90-degree angle, thus confirming that they are perpendicular.
Exploring the Square: A Special Case
A square is a special case of a rhombus (and also a special case of a rectangle). A square possesses all the properties of a parallelogram, a rhombus, and a rectangle. Therefore, the diagonals of a square are also perpendicular bisectors of each other. This reinforces the relationship we established with the rhombus.
Why are Diagonals Not Perpendicular in Other Parallelograms?
Consider a rectangle that is not a square. A rectangle is a parallelogram with four right angles. Its diagonals bisect each other, but they are not perpendicular unless the rectangle is also a square (i.e., all sides are equal). Similarly, a general parallelogram with unequal adjacent sides will not have perpendicular diagonals. The angles formed by the intersection of the diagonals will not be 90 degrees.
This difference highlights the importance of the equal side lengths condition that distinguishes a rhombus from other parallelograms. The equal side lengths are crucial for the proof of perpendicularity. Without this condition, the congruence of triangles crucial to the proof cannot be established.
Practical Applications and Problem-Solving
Understanding the relationship between diagonals and perpendicularity in parallelograms is essential for solving various geometric problems. For example:
-
Finding the area of a rhombus: The area of a rhombus can be efficiently calculated using the formula: Area = (1/2) * d1 * d2, where d1 and d2 are the lengths of the diagonals. This formula relies on the fact that the diagonals are perpendicular, dividing the rhombus into four congruent right-angled triangles.
-
Coordinate Geometry: When dealing with parallelograms in coordinate geometry, knowing whether the diagonals are perpendicular helps in determining the type of parallelogram and solving related problems. The dot product of the vectors representing the diagonals can be used to determine if they are perpendicular (dot product equals zero).
-
Vector Geometry: Similar to coordinate geometry, vector methods can be used to prove or disprove perpendicularity by analyzing the dot product of vectors representing the diagonals.
Advanced Considerations: Proofs using Vectors
Let's explore a more advanced proof using vector methods. This approach offers a concise and elegant way to demonstrate the perpendicularity of diagonals in a rhombus.
Let a and b be the vectors representing two adjacent sides of the rhombus. The diagonals can then be represented by the vectors a + b and a - b. If the diagonals are perpendicular, their dot product must be zero:
(a + b) • (a - b) = 0
Expanding this equation using the properties of the dot product:
a • a - a • b + b • a - b • b = 0
Since a • b = b • a, the equation simplifies to:
||a||² - ||b||² = 0
This implies that ||a||² = ||b||², which means ||a|| = ||b||. Since a and b represent the lengths of adjacent sides, this condition is only satisfied if all sides of the parallelogram are equal, indicating a rhombus. Therefore, the diagonals of a rhombus are perpendicular.
Conclusion: A Comprehensive Overview
The relationship between diagonals and perpendicularity in parallelograms is a rich topic with significant implications in various areas of geometry. While all parallelograms have diagonals that bisect each other, only rhombuses (and squares) possess the additional property of perpendicular diagonals. Understanding this distinction, along with the various methods of proof – including geometric proofs and vector methods – is essential for a solid grasp of geometric principles and their applications in problem-solving. This comprehensive exploration has equipped you with the knowledge and tools to confidently address questions concerning parallelogram diagonals and their perpendicularity. Remember, the key lies in recognizing the specific properties that define a rhombus and how these properties lead to the unique relationship between its diagonals.
Latest Posts
Latest Posts
-
Least Common Multiple Of 12 And 5
Apr 06, 2025
-
Cross Section Of A Sphere Parallel Perpendicular And Diagonal
Apr 06, 2025
-
The Main Circuit Board Of A Computer Is Called The
Apr 06, 2025
-
Mass Of An Alpha Particle In Kg
Apr 06, 2025
-
5 Letters Words With A And E
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Are Diagonals Perpendicular In A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
