Sum Of Exterior Angles Of A Quadrilateral
Juapaving
Apr 01, 2025 · 6 min read
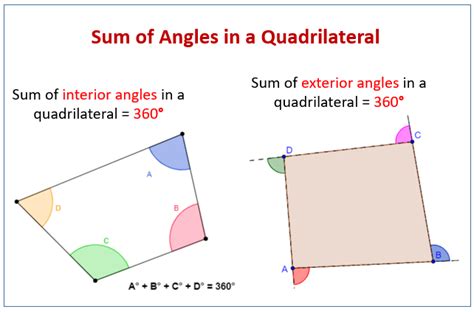
Table of Contents
The Sum of Exterior Angles of a Quadrilateral: A Comprehensive Exploration
The sum of exterior angles of any polygon, including quadrilaterals, is a fundamental concept in geometry. Understanding this concept opens doors to solving various geometric problems and strengthens your foundational understanding of shapes and angles. This article delves deep into the sum of exterior angles of a quadrilateral, exploring its proof, applications, and connections to broader geometrical principles.
Understanding Exterior Angles
Before we dive into the specifics of quadrilaterals, let's define what an exterior angle is. An exterior angle of a polygon is formed by extending one of its sides. It's the angle formed outside the polygon between the extended side and the adjacent side. Each vertex of a polygon has two exterior angles, one formed by extending each of the two sides meeting at that vertex. However, we typically work with one exterior angle per vertex, usually the one that forms a linear pair with the corresponding interior angle. Remember that a linear pair of angles adds up to 180 degrees.
The Sum of Exterior Angles of a Quadrilateral: The Proof
The sum of the exterior angles of any polygon, regardless of its shape or the number of sides, is always 360 degrees. This holds true for quadrilaterals as well. Let's explore a few ways to prove this fundamental geometric fact specifically for quadrilaterals:
Method 1: Using the Sum of Interior Angles
This method leverages the known fact that the sum of the interior angles of a quadrilateral is 360 degrees. Let's denote the interior angles of a quadrilateral as A, B, C, and D. Their sum is:
A + B + C + D = 360°
Now, let's consider the exterior angles. Let's denote the exterior angle at vertex A as A', at B as B', at C as C', and at D as D'. Since each exterior angle forms a linear pair with its corresponding interior angle, we have:
A + A' = 180° B + B' = 180° C + C' = 180° D + D' = 180°
Adding these equations together, we get:
(A + B + C + D) + (A' + B' + C' + D') = 720°
Since A + B + C + D = 360°, we can substitute this into the equation:
360° + (A' + B' + C' + D') = 720°
Subtracting 360° from both sides gives us:
A' + B' + C' + D' = 360°
This proves that the sum of the exterior angles of a quadrilateral is 360 degrees.
Method 2: Visual Demonstration and Rotation
Imagine walking around the perimeter of a quadrilateral, always turning at each corner to follow the path. At each corner, you turn through an angle equal to the exterior angle. After completing one full circuit, you will have turned a total of 360 degrees (a full circle). This visual representation clearly demonstrates that the sum of the exterior angles must equal 360°. This method is particularly helpful for intuitive understanding.
Applications of the Sum of Exterior Angles of a Quadrilateral
The principle that the sum of exterior angles of a quadrilateral equals 360 degrees has several practical applications:
-
Solving Geometric Problems: This principle is crucial for solving various geometry problems involving unknown angles in quadrilaterals. If you know some of the exterior angles, you can easily calculate the remaining ones. For example, if three exterior angles of a quadrilateral are given as 70°, 90°, and 110°, the fourth exterior angle can be calculated as 360° - (70° + 90° + 110°) = 90°.
-
Cartography and Navigation: The concept of exterior angles finds applications in navigation and cartography, where understanding directional changes is essential. Each turn represents an exterior angle, and understanding their sum is fundamental for precise path planning and map-making.
-
Engineering and Construction: In architecture and engineering, calculating angles is crucial for structural integrity. The sum of exterior angles of a quadrilateral helps in determining the precise angles needed when constructing structures with quadrilateral shapes. This aids in ensuring stability and proper alignment.
-
Computer Graphics and Game Design: In computer graphics and game development, the accurate calculation of angles is vital for rendering 2D and 3D shapes. The principle of exterior angle sums plays a role in creating realistic and accurate depictions of quadrilaterals and other polygons within virtual environments.
Extending the Concept: Polygons with More Than Four Sides
The principle of a 360-degree sum of exterior angles isn't limited to quadrilaterals; it extends to all polygons. The sum of exterior angles of any polygon, regardless of the number of sides, is always 360 degrees. This is a powerful and unifying concept in geometry. This holds true even for irregular polygons (polygons whose sides and angles are not all equal).
Relationship Between Interior and Exterior Angles
It's important to emphasize the close relationship between interior and exterior angles. They are supplementary angles, meaning that their sum is always 180 degrees. This relationship can be used to calculate unknown interior angles if exterior angles are known, and vice versa. For example, if an exterior angle is 120°, its corresponding interior angle is 180° - 120° = 60°. This interdependency is frequently used in solving problems involving both types of angles.
Types of Quadrilaterals and Exterior Angles
The sum of exterior angles remains constant at 360 degrees, regardless of the type of quadrilateral:
-
Square: A square has four equal sides and four equal angles (90 degrees each). Each exterior angle is 90 degrees, and their sum is 4 * 90° = 360°.
-
Rectangle: A rectangle has four right angles, so each exterior angle is also 90 degrees. The sum remains 360°.
-
Rhombus: A rhombus has four equal sides but angles are not necessarily equal. While the interior angles may vary, the sum of the exterior angles will still be 360°.
-
Parallelogram: A parallelogram has two pairs of parallel sides. Similar to a rhombus, the angles will vary but the exterior angles always sum to 360°.
-
Trapezoid (or Trapezium): A trapezoid has at least one pair of parallel sides. Regardless of the specific angles of the trapezoid, the sum of exterior angles will always be 360°.
-
Irregular Quadrilateral: Even for quadrilaterals with sides and angles of varying lengths and measures, the sum of exterior angles remains consistently 360°.
Advanced Applications and Further Exploration
The concept of exterior angles and their sum extends beyond basic geometry. It finds applications in:
-
Trigonometry: Exterior angles are used in various trigonometric calculations and proofs.
-
Calculus: In higher-level mathematics, the concepts related to angles and their sums form the foundation for more complex calculations.
-
Three-Dimensional Geometry: While this article focuses on two-dimensional shapes, the principles can be extended to three-dimensional solids and their faces.
Conclusion
The sum of exterior angles of a quadrilateral, always equaling 360 degrees, is a cornerstone of geometry. This fundamental concept is not merely a theoretical principle but a practical tool with wide-ranging applications across various fields. By understanding this principle, you enhance your problem-solving skills in geometry and appreciate the interconnectedness of mathematical concepts. From solving basic angle problems to contributing to advancements in engineering, computer graphics, and other fields, the seemingly simple concept of the exterior angles of a quadrilateral proves to be surprisingly profound. Its constant value provides a reliable foundation for countless calculations and theoretical explorations.
Latest Posts
Latest Posts
-
A Quadrilateral With One Pair Of Opposite Sides Parallel
Apr 02, 2025
-
Flip A Coin Roll A Die
Apr 02, 2025
-
Calculating Ka From A Titration Curve
Apr 02, 2025
-
5 Letter Words Starting With T H I
Apr 02, 2025
-
If 2 Matrix Multiplication Is 0
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Sum Of Exterior Angles Of A Quadrilateral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
