A Quadrilateral With One Pair Of Opposite Sides Parallel
Juapaving
Apr 02, 2025 · 6 min read
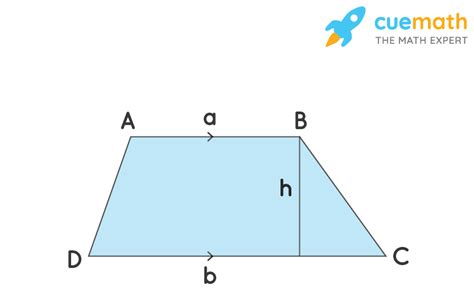
Table of Contents
A Quadrilateral with One Pair of Opposite Sides Parallel: Exploring Trapezoids
A quadrilateral, a polygon with four sides, offers a rich landscape for geometric exploration. Among the various types of quadrilaterals, those with at least one pair of parallel opposite sides hold a special place. This article delves deep into the fascinating world of trapezoids, exploring their properties, classifications, area calculations, and applications. We'll move beyond the basics, investigating advanced concepts and providing practical examples to solidify your understanding.
Defining the Trapezoid: More Than Just Parallel Sides
A trapezoid (also known as a trapezium in some regions) is defined as a quadrilateral with at least one pair of parallel sides. These parallel sides are called the bases of the trapezoid, often denoted as b₁ and b₂. The other two sides, which are not parallel, are called the legs. It's crucial to understand that the definition only requires one pair of parallel sides; the other pair can be parallel, but it's not a requirement. If both pairs of opposite sides are parallel, the trapezoid becomes a special case—a parallelogram.
This subtle distinction is important because it influences the properties and theorems associated with trapezoids. While parallelograms enjoy a symmetrical set of properties (opposite sides equal, opposite angles equal, diagonals bisect each other), trapezoids exhibit a more nuanced set of characteristics.
Key Properties of Trapezoids
Let's examine some of the key properties that define and distinguish trapezoids:
- At least one pair of parallel sides: This is the fundamental defining property.
- Base angles: Consecutive angles along the same base are supplementary (add up to 180°). This is a direct consequence of the parallel sides and the properties of transversal lines.
- Midsegment: The line segment connecting the midpoints of the legs is parallel to the bases and its length is the average of the lengths of the bases. This midsegment is also known as the median. This property is particularly useful in calculations involving the trapezoid's dimensions.
- Area: The area of a trapezoid is calculated using the formula: Area = ½(b₁ + b₂)h, where b₁ and b₂ are the lengths of the bases, and h is the height (the perpendicular distance between the bases).
Classifying Trapezoids: Beyond the Basics
While the fundamental definition of a trapezoid is straightforward, we can further classify trapezoids based on the lengths of their legs and the measure of their angles:
1. Isosceles Trapezoids: Symmetry and Elegance
An isosceles trapezoid is a trapezoid where the legs are congruent (equal in length). This symmetry leads to some additional properties:
- Base angles are congruent: The two angles at each base are equal in measure.
- Diagonals are congruent: The lengths of the diagonals are equal.
- Reflection symmetry: An isosceles trapezoid exhibits reflection symmetry across a line perpendicular to both bases and passing through their midpoints.
These properties make isosceles trapezoids particularly interesting from a geometrical perspective, and they often feature prominently in geometry problems.
2. Right Trapezoids: A Right Angle Perspective
A right trapezoid is a trapezoid with at least one right angle. This seemingly simple addition introduces several practical implications for calculations. The height of a right trapezoid is simply the length of one of its legs. This simplification makes area calculations particularly straightforward.
3. Scalene Trapezoids: The General Case
A scalene trapezoid is a trapezoid that doesn't fall into either of the above categories. It has legs of unequal length, and its angles are not necessarily congruent. This is the most general type of trapezoid, encompassing a vast range of shapes and dimensions.
Calculating the Area of a Trapezoid: Methods and Applications
The formula for the area of a trapezoid, Area = ½(b₁ + b₂)h, is fundamental. However, the challenge often lies in determining the height (h) when it's not directly given. Various trigonometric methods can be employed, depending on the information provided. For example, if the legs and the base angles are known, trigonometric functions like sine and cosine can be used to calculate the height.
Example: Calculating the Area of an Isosceles Trapezoid
Consider an isosceles trapezoid with bases of length 6 cm and 10 cm, and legs of length 5 cm. To find the area, we first need to determine the height. We can do this by drawing an altitude from one of the vertices to the longer base, creating two right-angled triangles. Using the Pythagorean theorem, we can find the height. The height can also be derived using the properties of isosceles trapezoids.
Advanced Concepts and Theorems: Delving Deeper into Trapezoids
Beyond the basics, several advanced theorems and concepts relate to trapezoids, expanding their relevance in higher-level mathematics:
1. Ptolemy's Theorem for Cyclic Trapezoids
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. If a trapezoid is cyclic, it must be an isosceles trapezoid. This connection between cyclic quadrilaterals and isosceles trapezoids is elegantly expressed through Ptolemy's Theorem.
2. Trapezoids in Coordinate Geometry
Trapezoids can be efficiently analyzed using coordinate geometry. By assigning coordinates to the vertices, we can use distance formulas and slope calculations to verify properties, find areas, and solve geometric problems related to trapezoids.
3. Trapezoids in Calculus: Approximating Areas
Trapezoids play a significant role in numerical integration techniques in calculus. The trapezoidal rule, a method for approximating the definite integral of a function, uses trapezoids to estimate the area under a curve. This demonstrates the practical application of trapezoidal geometry in advanced mathematical fields.
Applications of Trapezoids in Real World: From Architecture to Art
Trapezoids are surprisingly common in the real world, appearing in various structures and designs:
- Architecture: Trapezoidal shapes are often incorporated into building designs for both aesthetic and structural reasons. Think of the unique rooflines of some buildings.
- Civil Engineering: In civil engineering, trapezoidal shapes are used in cross-sections of canals and other waterways to optimize water flow and structural stability.
- Art and Design: The trapezoid's unique visual properties have inspired artists and designers across various mediums. The dynamic and asymmetric nature of trapezoids offers creative possibilities.
- Nature: While less obvious, approximations of trapezoidal shapes can be found in nature, albeit often irregularly. Certain geological formations and even some leaves exhibit approximate trapezoidal shapes.
Conclusion: The Enduring Relevance of Trapezoids
From their fundamental geometric properties to their advanced applications in calculus and real-world scenarios, trapezoids demonstrate the enduring importance of seemingly simple shapes. Understanding their characteristics, classifications, and properties provides a robust foundation for tackling complex geometric problems and appreciating the elegance and practicality of mathematics in our world. This exploration of trapezoids serves as a testament to the beauty and power of geometrical understanding, highlighting its relevance across various scientific and artistic disciplines. The depth and versatility of trapezoid geometry offer continuous opportunities for exploration and discovery, making it a captivating topic for students and enthusiasts alike. The continued study and application of trapezoid properties will undoubtedly lead to further advancements in various fields, confirming the enduring relevance of this seemingly simple yet richly complex geometrical figure.
Latest Posts
Latest Posts
-
Mm Cm M Km Conversion Chart
Apr 03, 2025
-
Lowest Common Multiple Of 16 And 20
Apr 03, 2025
-
What Organelle Is Only Found In Animal Cells
Apr 03, 2025
-
Is A Square Also A Parallelogram
Apr 03, 2025
-
1 Out Of 10 As A Percentage
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about A Quadrilateral With One Pair Of Opposite Sides Parallel . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
