Square Square Roots Cubes And Cube Roots
Juapaving
Apr 02, 2025 · 5 min read
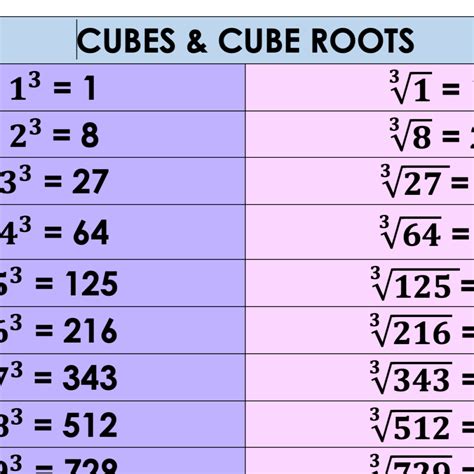
Table of Contents
Square Roots, Cubes, and Cube Roots: A Comprehensive Guide
Understanding square roots, cubes, and cube roots is fundamental to grasping many mathematical concepts. These operations are essential in algebra, geometry, calculus, and numerous real-world applications. This comprehensive guide will explore these concepts, providing clear explanations, examples, and practical applications to solidify your understanding.
What are Squares and Square Roots?
A square of a number is the result of multiplying that number by itself. For example, the square of 5 (written as 5²) is 5 * 5 = 25. In general terms, the square of a number 'x' is denoted as x².
A square root, conversely, is the number that, when multiplied by itself, gives the original number. For instance, the square root of 25 (written as √25) is 5 because 5 * 5 = 25. Every positive number has two square roots: one positive and one negative. For example, the square roots of 25 are +5 and -5, since both 5 * 5 = 25 and (-5) * (-5) = 25. However, when we use the square root symbol (√), we usually refer to the principal square root, which is the positive square root.
Understanding Perfect Squares
A perfect square is a number that can be obtained by squaring an integer. Examples of perfect squares include:
- 1 (1²)
- 4 (2²)
- 9 (3²)
- 16 (4²)
- 25 (5²)
- and so on...
Calculating Square Roots
Calculating square roots can be done using various methods:
- Mental Calculation: For smaller numbers, you might be able to determine the square root mentally.
- Calculators: Most calculators have a dedicated square root function (√).
- Estimation: You can estimate the square root by finding the nearest perfect squares. For example, to estimate √20, you know that √16 = 4 and √25 = 5, so √20 is somewhere between 4 and 5.
- Long Division Method: A more advanced method for manual calculation is the long division method for square roots.
Real-World Applications of Squares and Square Roots
Squares and square roots have various applications in:
- Geometry: Calculating the area of a square (side²) or the length of the hypotenuse of a right-angled triangle using the Pythagorean theorem (a² + b² = c²).
- Physics: Many physics formulas involve squares and square roots, such as calculating velocity, acceleration, or energy.
- Engineering: Used extensively in structural calculations and designing various engineering systems.
What are Cubes and Cube Roots?
Similar to squares and square roots, we have cubes and cube roots. A cube of a number is the result of multiplying the number by itself three times. For example, the cube of 2 (written as 2³) is 2 * 2 * 2 = 8. In general, the cube of a number 'x' is denoted as x³.
A cube root, conversely, is the number that, when multiplied by itself three times, gives the original number. The cube root of 8 (written as ³√8) is 2 because 2 * 2 * 2 = 8. Unlike square roots, every real number has only one real cube root. For example, the cube root of -8 is -2 because (-2) * (-2) * (-2) = -8.
Understanding Perfect Cubes
A perfect cube is a number that can be obtained by cubing an integer. Examples include:
- 1 (1³)
- 8 (2³)
- 27 (3³)
- 64 (4³)
- 125 (5³)
- and so on...
Calculating Cube Roots
Calculating cube roots can also be done in various ways:
- Mental Calculation: For smaller numbers, it's often possible to determine the cube root mentally.
- Calculators: Scientific calculators typically have a cube root function (³√).
- Estimation: Similar to square roots, you can estimate cube roots by finding the nearest perfect cubes.
- Numerical Methods: More advanced numerical methods exist for calculating cube roots with high precision.
Real-World Applications of Cubes and Cube Roots
Cubes and cube roots appear in:
- Geometry: Calculating the volume of a cube (side³).
- Physics: Many physics formulas, including those related to volume, density, and some aspects of fluid dynamics, involve cubes and cube roots.
- Chemistry: Used in stoichiometry calculations and understanding the relationships between substances in chemical reactions.
Comparing Squares, Cubes, and Their Roots
Both squares and cubes represent powers of a number, with squares being the second power (x²) and cubes being the third power (x³). Square roots and cube roots are the inverse operations of squaring and cubing, respectively. While every positive number has two square roots, every real number has only one real cube root.
Advanced Concepts and Extensions
The concepts of squares, cubes, and their roots extend to higher powers. We can talk about fourth powers (x⁴), fifth powers (x⁵), and so on, along with their corresponding roots. The general notation for nth root is ⁿ√x.
Solving Equations Involving Squares and Cubes
Many mathematical problems involve solving equations with squares and cubes. Here are some examples:
-
Solving Quadratic Equations: These equations involve x². The solutions can be found using the quadratic formula or factoring.
-
Solving Cubic Equations: These equations involve x³. Solving cubic equations can be more complex, often requiring numerical methods or advanced algebraic techniques.
Practical Exercises
To solidify your understanding, try the following exercises:
- Find the square and cube of the following numbers: 3, 7, 10, and 12.
- Find the square root and cube root of the following numbers: 81, 64, 1000, and 216.
- Solve the quadratic equation: x² - 5x + 6 = 0.
- Estimate the square root of 70 and the cube root of 100.
Conclusion
Understanding squares, cubes, and their roots is crucial for success in various mathematical fields and real-world applications. This guide has provided a solid foundation, but remember that continued practice and exploration are key to mastering these fundamental concepts. By understanding these concepts and practicing solving problems, you'll develop a stronger mathematical foundation for more complex concepts. Remember to utilize online resources and textbooks for further learning and to solve more complex problems related to squares, cubes, and their roots. The journey of mastering these concepts is continuous, so keep practicing and learning!
Latest Posts
Latest Posts
-
How Many Hearts Does Worm Have
Apr 03, 2025
-
5 2 Simplified As A Mixed Number
Apr 03, 2025
-
Is 87 A Composite Or Prime Number
Apr 03, 2025
-
Does A Eukaryotic Cell Have Ribosomes
Apr 03, 2025
-
Equation For Charging And Discharging Of Capacitor
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Square Square Roots Cubes And Cube Roots . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
