Equation For Charging And Discharging Of Capacitor
Juapaving
Apr 03, 2025 · 7 min read
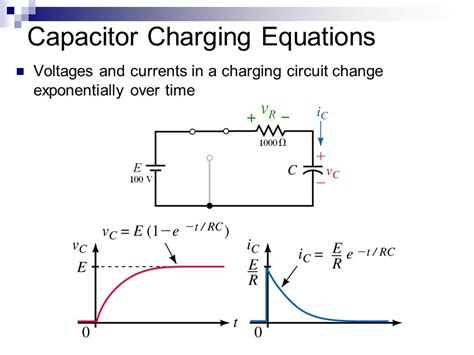
Table of Contents
The Complete Guide to Capacitor Charging and Discharging Equations
Capacitors are fundamental passive electronic components that store electrical energy in an electric field. Understanding how they charge and discharge is crucial for anyone working with electronics. This comprehensive guide delves into the equations governing these processes, exploring their derivations, applications, and practical considerations.
Understanding Capacitance and the Basic Principles
Before diving into the equations, let's establish a firm grasp of capacitance. Capacitance (C) is a measure of a capacitor's ability to store charge. It's defined as the ratio of the charge (Q) stored on each plate to the potential difference (V) across the plates:
C = Q/V
The unit of capacitance is the Farad (F), representing one coulomb of charge per volt. In practice, capacitors typically range from picofarads (pF) to farads (F).
The behavior of a capacitor during charging and discharging is governed by the fundamental principles of electromagnetism and circuit theory. Essentially, current flows into or out of the capacitor to change the charge stored on its plates, resulting in a change in voltage across the plates. This process is not instantaneous; it takes time.
The Charging of a Capacitor
When a capacitor is connected to a DC voltage source through a resistor, it begins to charge. The voltage across the capacitor increases gradually, approaching the source voltage asymptotically. This process is described by the following equation:
V<sub>c</sub>(t) = V<sub>s</sub>(1 - e<sup>-t/RC</sup>)
Where:
- V<sub>c</sub>(t) is the voltage across the capacitor at time t.
- V<sub>s</sub> is the source voltage.
- t is the time elapsed since the charging began.
- R is the resistance in the circuit (in ohms).
- C is the capacitance of the capacitor (in farads).
- e is the base of the natural logarithm (approximately 2.718).
- RC is the time constant (τ), representing the time it takes for the capacitor to charge to approximately 63.2% of the source voltage.
Derivation of the Charging Equation
This equation is derived from Kirchhoff's voltage law and the definition of capacitance. The voltage across the resistor (V<sub>R</sub>) and the voltage across the capacitor (V<sub>c</sub>) must sum to the source voltage (V<sub>s</sub>):
V<sub>s</sub> = V<sub>R</sub> + V<sub>c</sub>
Using Ohm's law (V<sub>R</sub> = IR) and the definition of capacitance (Q = CV<sub>c</sub>), we can rewrite this as:
V<sub>s</sub> = IR + CV<sub>c</sub>(dq/dt)
Since I = dq/dt (the rate of change of charge is the current), we get a first-order differential equation:
V<sub>s</sub> = R(dq/dt) + (q/C)
Solving this differential equation with the initial condition q(0) = 0 (the capacitor is initially uncharged) yields the equation for the charge on the capacitor as a function of time:
q(t) = CV<sub>s</sub>(1 - e<sup>-t/RC</sup>)
Substituting this back into the capacitance equation (V<sub>c</sub> = q/C) gives us the voltage equation presented earlier.
Time Constant (τ = RC) and its Significance
The time constant, τ = RC, is a crucial parameter in capacitor charging. It determines the rate at which the capacitor charges. After one time constant (t = τ), the capacitor voltage reaches approximately 63.2% of the source voltage. After five time constants (t = 5τ), the capacitor is considered to be fully charged, reaching approximately 99.3% of the source voltage.
Practical Applications of Capacitor Charging
Capacitor charging finds applications in a vast range of electronic circuits, including:
- Power supplies: Smoothing out fluctuations in DC voltage.
- Timing circuits: Generating precise time delays.
- Flash photography: Storing energy for a brief, high-power burst.
- Sampling circuits: Holding a voltage level for a specific period.
- Energy storage systems: In larger applications like electric vehicles and renewable energy systems.
The Discharging of a Capacitor
When a charged capacitor is connected across a resistor, it begins to discharge. The voltage across the capacitor decreases gradually, approaching zero asymptotically. This process is described by the following equation:
V<sub>c</sub>(t) = V<sub>0</sub>e<sup>-t/RC</sup>
Where:
- V<sub>c</sub>(t) is the voltage across the capacitor at time t.
- V<sub>0</sub> is the initial voltage across the capacitor (at t = 0).
- t is the time elapsed since the discharging began.
- R is the resistance in the circuit (in ohms).
- C is the capacitance of the capacitor (in farads).
- e is the base of the natural logarithm (approximately 2.718).
- RC is the time constant (τ), having the same meaning as in charging.
Derivation of the Discharging Equation
The derivation is similar to the charging case, but with different initial conditions. Starting with Kirchhoff's voltage law:
0 = V<sub>R</sub> + V<sub>c</sub>
And substituting Ohm's law and the definition of capacitance, we get:
0 = R(dq/dt) + (q/C)
Solving this differential equation with the initial condition q(0) = CV<sub>0</sub> (the capacitor is initially charged to V<sub>0</sub>) yields the equation for the charge on the capacitor during discharge:
q(t) = CV<sub>0</sub>e<sup>-t/RC</sup>
Again, substituting into the capacitance equation (V<sub>c</sub> = q/C) gives us the voltage equation for discharging.
Time Constant (τ = RC) in Discharging
The time constant plays the same role in discharging as in charging. After one time constant (t = τ), the voltage across the capacitor drops to approximately 36.8% of its initial value. After five time constants (t = 5τ), the capacitor is considered to be fully discharged, with the voltage dropping to approximately 0.7% of its initial value.
Practical Applications of Capacitor Discharging
Capacitor discharging is equally important in various applications, including:
- Timing circuits: Creating precise time delays in various applications like blinking LEDs.
- Pulse generation: Producing short, controlled bursts of voltage.
- Energy harvesting: Releasing stored energy in a controlled manner.
- Defibrillators: Delivering a high-voltage pulse to restart a heart.
- Camera flashes: Discharging stored energy to create the flash.
Factors Affecting Charging and Discharging Times
Several factors influence the charging and discharging times of a capacitor:
- Capacitance (C): Larger capacitance leads to longer charging and discharging times.
- Resistance (R): Larger resistance also leads to longer charging and discharging times.
- Temperature: Temperature can affect the resistance of the components, indirectly affecting the charging and discharging times.
- Capacitor type: Different types of capacitors exhibit varying charging and discharging characteristics. Electrolytic capacitors, for example, generally have longer charging times than ceramic capacitors.
Beyond the Simple RC Circuit: More Complex Scenarios
The equations presented above describe the behavior of a simple RC circuit. In more complex circuits, involving multiple capacitors and resistors, or other components like inductors, the analysis becomes significantly more challenging. Techniques like Laplace transforms and nodal analysis are often employed to solve these complex circuits.
Practical Considerations and Troubleshooting
When working with capacitors, several practical considerations are important:
- Voltage ratings: Ensure that the capacitor's voltage rating is sufficient for the applied voltage to prevent damage.
- Tolerance: Capacitors have tolerances, meaning their actual capacitance may differ slightly from their rated value.
- ESR (Equivalent Series Resistance): All capacitors have some internal resistance, which can affect their charging and discharging behavior, especially at higher frequencies.
- Leakage current: Some capacitors exhibit a small leakage current, meaning they slowly discharge even when not connected to a circuit.
Troubleshooting issues related to capacitor charging and discharging often involves checking the circuit for shorts, open circuits, faulty components, and incorrect component values. Using a multimeter to measure voltage and resistance can help pinpoint the problem.
Conclusion
The equations for charging and discharging capacitors are fundamental to understanding the behavior of these essential electronic components. This comprehensive guide has covered the derivation and application of these equations, along with practical considerations and troubleshooting techniques. Mastery of these concepts is crucial for anyone designing, building, or troubleshooting electronic circuits. Remember that while these equations provide a solid foundation, real-world circuits often involve complexities requiring more advanced analysis techniques. Continual learning and hands-on experience are key to becoming proficient in this field.
Latest Posts
Latest Posts
-
A Force Is A Scalar Quantity True False
Apr 04, 2025
-
A Sound Wave Is An Example Of A Longitudinal Wave
Apr 04, 2025
-
Fundamental Building Block Of All Matter
Apr 04, 2025
-
Exterior Angle Of A Regular Hexagon
Apr 04, 2025
-
What Is The Radius Of Circle With Centre N
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Equation For Charging And Discharging Of Capacitor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
