Square Root Of 160 In Radical Form
Juapaving
Mar 31, 2025 · 5 min read
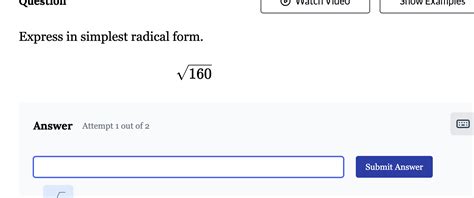
Table of Contents
Unveiling the Mystery: Understanding the Square Root of 160 in Radical Form
The seemingly simple question, "What is the square root of 160 in radical form?" opens a door to a fascinating exploration of number theory and radical simplification. While a calculator will readily provide a decimal approximation, expressing the square root of 160 in its simplest radical form reveals a deeper mathematical understanding. This comprehensive guide will dissect this problem, explaining the process step-by-step, exploring related concepts, and offering practical exercises to solidify your grasp on radical simplification.
Understanding Square Roots and Radicals
Before diving into the specifics of √160, let's refresh our understanding of square roots and radicals. A square root of a number x is a number that, when multiplied by itself, equals x. The symbol √ represents the principal (non-negative) square root. A radical is an expression containing a radical symbol (√), indicating a root of a number. The number inside the radical symbol is called the radicand.
For example, √25 = 5 because 5 * 5 = 25. The number 25 is the radicand, and 5 is the square root. Not all numbers have perfect square roots (integers). Numbers like 2, 3, 7, etc., have irrational square roots, meaning their decimal representations go on forever without repeating.
Prime Factorization: The Key to Simplification
The key to simplifying radicals like √160 lies in prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 160:
- Divide by 2: 160 ÷ 2 = 80
- Divide by 2 again: 80 ÷ 2 = 40
- Divide by 2 again: 40 ÷ 2 = 20
- Divide by 2 again: 20 ÷ 2 = 10
- Divide by 2 again: 10 ÷ 2 = 5
- 5 is a prime number: We stop here.
Therefore, the prime factorization of 160 is 2 * 2 * 2 * 2 * 2 * 5 = 2<sup>5</sup> * 5.
Simplifying √160
Now that we have the prime factorization of 160 (2<sup>5</sup> * 5), we can simplify √160:
- Rewrite the radical using the prime factorization: √(2<sup>5</sup> * 5)
- Separate the perfect squares: We can rewrite 2<sup>5</sup> as 2<sup>4</sup> * 2. 2<sup>4</sup> is a perfect square (2<sup>4</sup> = 16).
- Simplify: √(2<sup>4</sup> * 2 * 5) = √(2<sup>4</sup>) * √(2 * 5)
- Take the square root of the perfect square: √(2<sup>4</sup>) = 2<sup>4/2</sup> = 2<sup>2</sup> = 4
- Combine: 4√(10)
Therefore, the simplest radical form of √160 is 4√10.
Working with More Complex Radicals
The process outlined above can be applied to more complex radicals. The core principle remains the same: find the prime factorization of the radicand and identify perfect square factors to simplify the expression.
Let's consider another example: √72
- Prime factorization of 72: 72 = 2<sup>3</sup> * 3<sup>2</sup>
- Identify perfect squares: 3<sup>2</sup> is a perfect square. We can also express 2<sup>3</sup> as 2<sup>2</sup> * 2.
- Rewrite: √(2<sup>2</sup> * 2 * 3<sup>2</sup>)
- Simplify: √(2<sup>2</sup>) * √(3<sup>2</sup>) * √2 = 2 * 3 * √2 = 6√2
Therefore, √72 simplifies to 6√2.
Adding and Subtracting Radicals
Once you understand simplification, you can move on to operations with radicals. Adding and subtracting radicals requires that they have the same radicand. If the radicands are different, you need to simplify the radicals first and then check again.
For example:
3√2 + 5√2 = 8√2
However, if you have 3√2 + √8, you first need to simplify √8 (which is 2√2), then you can add them together: 3√2 + 2√2 = 5√2.
Multiplying and Dividing Radicals
Multiplication and division of radicals also involve simplifying. Remember that √a * √b = √(a*b) and √a / √b = √(a/b).
Multiplication Example:
√2 * √6 = √(2*6) = √12 = 2√3
Division Example:
√18 / √2 = √(18/2) = √9 = 3
Practical Applications and Real-World Examples
Understanding radical simplification isn't just an academic exercise; it has practical applications in various fields:
-
Geometry: Calculating the diagonal of a square, the hypotenuse of a right-angled triangle, or the area of various shapes often involves square roots and radical expressions.
-
Physics: Many physics equations, particularly those dealing with motion, energy, and waves, utilize square roots.
-
Engineering: Structural design, electrical circuits, and various engineering disciplines frequently involve calculations requiring radical simplification.
Further Exploration and Challenges
To further solidify your understanding, try simplifying the following radicals:
- √288
- √48
- √125
- √320
- √500
Remember the steps: prime factorization, identify perfect squares, simplify, and combine. These exercises will build your proficiency and confidence in handling radical expressions.
Conclusion: Mastering Radical Simplification
Mastering the simplification of radicals, such as finding the square root of 160 in its simplest radical form (4√10), is a crucial skill in mathematics. Through understanding prime factorization and the properties of square roots, we can elegantly express these numbers and use them effectively in various mathematical and real-world applications. The process requires practice, but with consistent effort, you can achieve proficiency in simplifying radicals and navigate more complex mathematical problems with confidence. Remember to break down the problem systematically, and the solution will become clear.
Latest Posts
Latest Posts
-
7 875 Rounded To The Nearest Hundredth
Apr 02, 2025
-
How Many Parents Are Needed For Asexual Reproduction
Apr 02, 2025
-
Least Common Multiple Of 35 And 49
Apr 02, 2025
-
What Is Meant By The Simplest Formula Of A Compound
Apr 02, 2025
-
What Is The Largest Gland In The Body
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 160 In Radical Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
