Least Common Multiple Of 35 And 49
Juapaving
Apr 02, 2025 · 5 min read
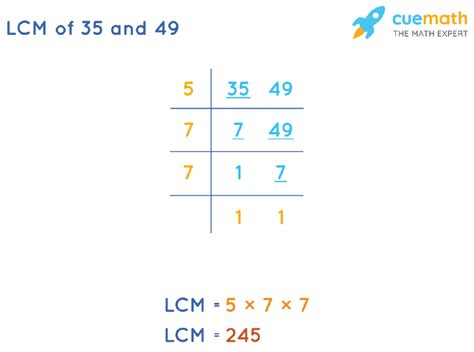
Table of Contents
Finding the Least Common Multiple (LCM) of 35 and 49: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in number theory with wide-ranging applications in mathematics, computer science, and even music theory. Understanding how to find the LCM is crucial for solving various problems involving fractions, ratios, and rhythmic patterns. This article will delve into the detailed process of calculating the LCM of 35 and 49, exploring different methods and providing a comprehensive understanding of the underlying principles.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 35 and 49, let's establish a firm grasp of the concept itself. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, making 6 the LCM of 2 and 3.
Methods for Finding the LCM
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. We will explore three primary approaches:
1. Listing Multiples Method
This is the most straightforward method, particularly suitable for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple.
Let's apply this method to find the LCM of 35 and 49:
- Multiples of 35: 35, 70, 105, 140, 175, 210, 245, 280, 315, 350, 385, 420...
- Multiples of 49: 49, 98, 147, 196, 245, 294, 343, 392, 441...
Notice that 245 appears in both lists. However, a smaller common multiple exists: 245. Therefore, the LCM of 35 and 49 is 245. This method becomes less efficient with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Let's break down 35 and 49 into their prime factors:
- 35 = 5 x 7
- 49 = 7 x 7 = 7²
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The prime factors are 5 and 7.
- The highest power of 5 is 5¹ (from 35).
- The highest power of 7 is 7² (from 49).
Therefore, the LCM(35, 49) = 5¹ x 7² = 5 x 49 = 245
This method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The relationship between the LCM and GCD is given by the formula:
LCM(a, b) x GCD(a, b) = a x b
To use this method, we first need to find the GCD of 35 and 49. We can use the Euclidean algorithm for this:
- Divide the larger number (49) by the smaller number (35): 49 ÷ 35 = 1 with a remainder of 14.
- Replace the larger number with the smaller number (35) and the smaller number with the remainder (14): 35 ÷ 14 = 2 with a remainder of 7.
- Repeat: 14 ÷ 7 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 7.
Now, we can use the formula:
LCM(35, 49) = (35 x 49) / GCD(35, 49) = (35 x 49) / 7 = 245
This method is also efficient and relies on a well-established algorithm for finding the GCD.
Applications of LCM
The LCM has numerous applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Scheduling Problems: Determining when events with different periodicities will occur simultaneously (e.g., two buses arriving at the same stop at the same time).
-
Music Theory: Calculating the least common multiple of note durations to find the length of a rhythmic cycle.
-
Computer Science: Synchronization of processes in parallel computing.
-
Engineering: Designing systems with components operating at different frequencies.
Further Exploration: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply include all prime factors from all numbers, using the highest power of each. For the GCD method, you can iteratively find the LCM of pairs of numbers.
For instance, to find the LCM of 35, 49, and say, 14:
-
Prime Factorization:
- 35 = 5 x 7
- 49 = 7²
- 14 = 2 x 7
-
Combine Prime Factors: The highest powers are 2¹, 5¹, and 7².
-
Calculate LCM: LCM(35, 49, 14) = 2¹ x 5¹ x 7² = 2 x 5 x 49 = 490
Conclusion: Mastering the LCM
Finding the least common multiple is a fundamental skill with broad applications. While the listing multiples method is intuitive for small numbers, the prime factorization and GCD methods offer greater efficiency and mathematical insight, particularly for larger numbers and more complex problems. Understanding these methods empowers you to confidently tackle a wide range of mathematical challenges, from basic arithmetic to more advanced applications in various fields. By mastering the concept of LCM, you are building a strong foundation in number theory and its practical applications. Remember that consistent practice is key to developing fluency and expertise in this essential mathematical concept. The more you work with LCM problems, the more comfortable and efficient you will become.
Latest Posts
Latest Posts
-
A Sphere Is Inscribed In A Cube
Apr 03, 2025
-
Balanced Equation Of Hcl And Naoh
Apr 03, 2025
-
What Is 0 35 As A Fraction
Apr 03, 2025
-
Least Common Multiple Of 15 And 18
Apr 03, 2025
-
Do Both Plant And Animal Cells Have Plasma Membrane
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 35 And 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
