Right Isosceles Triangles Into Cube Frame
Juapaving
Apr 05, 2025 · 6 min read
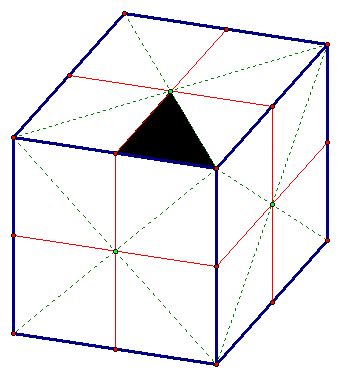
Table of Contents
Right Isosceles Triangles Inscribed in a Cube Frame: A Geometric Exploration
The seemingly simple cube, with its six square faces and twelve edges, holds a wealth of hidden geometric relationships. One fascinating exploration involves inscribing right isosceles triangles within the cube's framework. This seemingly straightforward task opens up a surprising array of possibilities, leading to intriguing geometric properties and challenging problems. This article will delve into the various ways right isosceles triangles can be inscribed within a cube, exploring their unique characteristics and the mathematical principles that govern them.
Understanding the Basics: Cubes and Right Isosceles Triangles
Before we embark on our exploration, let's establish a firm understanding of the fundamental elements:
The Cube: A cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. All its edges are of equal length, and all its angles are right angles (90 degrees).
The Right Isosceles Triangle: A right isosceles triangle is a triangle with one right angle (90 degrees) and two equal sides (legs). The two equal sides are adjacent to the right angle, and the third side (the hypotenuse) is opposite the right angle and is always longer than the legs. The angles opposite the equal sides are also equal, both measuring 45 degrees.
Inscribing Triangles: Different Approaches
There are several ways to inscribe a right isosceles triangle within a cube's structure. Let's examine a few prominent approaches:
1. Triangles formed by using edges and diagonals of faces
One straightforward method involves utilizing the cube's edges and the diagonals of its faces. Consider a face of the cube. We can form a right isosceles triangle by connecting two adjacent vertices (forming one leg) and then connecting one of those vertices to the opposite vertex on the same face (forming the other leg and hypotenuse). This gives us a right isosceles triangle with legs equal to the edge length of the cube. We can repeat this process on any of the cube's six faces.
Properties:
- The legs are equal to the cube's edge length.
- The hypotenuse is equal to the diagonal of a face (√2 times the edge length).
- The area of the triangle is half the square of the cube's edge length.
2. Triangles using diagonals of faces and cube diagonals
A more complex approach involves using the diagonals of the cube's faces and the main diagonal of the cube. Connecting two vertices of the cube that are furthest apart will form the cube's main diagonal. This diagonal can then be used as one leg of the triangle. By connecting a midpoint of an edge on the same face that contains the other endpoint of the diagonal to the other endpoint of the main diagonal that's used as the leg, you can form another leg. This creates a right isosceles triangle.
Properties:
- The legs have different lengths – one being the face diagonal and the other the cube diagonal.
- The triangle’s area is more complex to calculate than with method 1.
3. Triangles formed by connecting vertices and the center of the cube
Another interesting method uses the cube's center. Consider connecting the center of the cube to two opposite vertices of one face, and then creating a triangle using these three points. If the connection from the center is carefully constructed, it's possible to create a right isosceles triangle.
Properties:
- The lengths of the legs depend on the cube's edge length and the distance from the center to a face vertex.
- This approach requires more calculations to determine the precise properties of the triangles.
Exploring the Mathematical Relationships
Let's delve into the mathematical relationships that govern these inscribed triangles. The Pythagorean theorem, a cornerstone of geometry, plays a vital role.
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs). In our case, for the triangles formed using the cube's edges and face diagonals (method 1), we have:
Hypotenuse² = Leg² + Leg²
Since the legs are equal in length (let's denote the cube's edge length as 'a'), this simplifies to:
Hypotenuse² = a² + a² = 2a²
Therefore, the hypotenuse = √2a.
This illustrates the relationship between the cube's edge length and the hypotenuse of the right isosceles triangle formed by its edges and face diagonals.
For the triangles formed using more complex combinations of edges, face diagonals, and space diagonals (method 2 and 3), the Pythagorean theorem will still apply, but the calculations become more involved, requiring a deeper understanding of three-dimensional coordinate geometry. This is because the legs are no longer simply equal to the edge lengths or face diagonals.
Applications and Further Exploration
The exploration of right isosceles triangles inscribed in a cube frame extends beyond simple geometry. The concepts discussed have applications in various fields, including:
- Computer Graphics and 3D Modeling: Understanding these geometric relationships is crucial for creating realistic 3D models and computer-generated imagery. The ability to precisely define and manipulate triangles within a cube frame is fundamental to many 3D modeling techniques.
- Engineering and Architecture: The principles of spatial geometry, as illustrated in this exploration, are vital in structural design, especially when dealing with cubic or cuboid structures.
- Crystallography: The structure of many crystals exhibits cubic symmetry. Understanding the geometric properties of triangles inscribed within a cube can aid in the analysis of crystal structures.
Beyond the scenarios presented, further exploration might involve:
- Investigating the maximum and minimum areas achievable for right isosceles triangles inscribed within a cube. This could involve exploring different orientations and combinations of vertices.
- Exploring similar relationships with other regular polyhedra. The concepts discussed could be applied to other geometric solids such as tetrahedra, octahedra, and dodecahedra, leading to new and interesting geometric discoveries.
- Exploring the use of different coordinate systems. Applying Cartesian or other coordinate systems could simplify the calculations and analyses involved in more complex configurations.
Conclusion
The seemingly simple task of inscribing right isosceles triangles within a cube frame opens a door to a fascinating world of geometric exploration. The intricate interplay between the cube's dimensions and the triangle's properties highlights the beauty and complexity of spatial geometry. Understanding these relationships enhances our appreciation for geometric principles and has practical implications in various fields, encouraging further study and exploration. The mathematical principles discussed here form a robust foundation for more advanced investigations into higher-dimensional geometry and its applications. The journey from simple observation to complex mathematical analysis demonstrates the power of geometry as a tool for understanding and solving complex problems. The beauty lies not just in the solutions, but in the process of discovery itself.
Latest Posts
Latest Posts
-
A Particle Executes Simple Harmonic Motion
Apr 05, 2025
-
2 9 As A Decimal And Percent
Apr 05, 2025
-
Force Is A Scalar Or Vector Quantity
Apr 05, 2025
-
Are Diagonals Perpendicular In A Parallelogram
Apr 05, 2025
-
5 Letter Word Starts With Thi
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Right Isosceles Triangles Into Cube Frame . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
