Moment Of Inertia Of Quarter Circle
Juapaving
Mar 28, 2025 · 5 min read
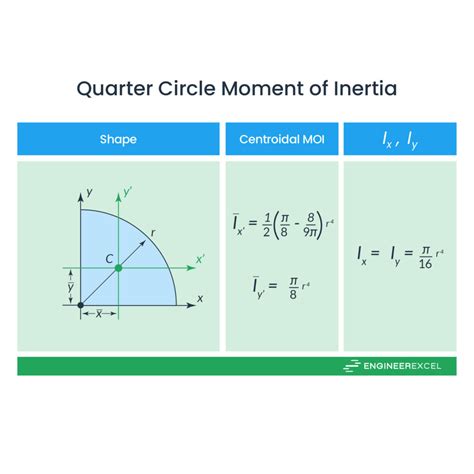
Table of Contents
Moment of Inertia of a Quarter Circle: A Comprehensive Guide
The moment of inertia, a crucial concept in physics and engineering, quantifies an object's resistance to changes in its rotation. Understanding the moment of inertia is vital for analyzing rotational motion, predicting dynamic behavior, and designing stable structures. This comprehensive guide delves into the calculation of the moment of inertia for a quarter circle, exploring various approaches and providing a detailed explanation of the underlying principles.
What is Moment of Inertia?
Before diving into the specifics of a quarter circle, let's establish a firm understanding of the moment of inertia itself. It's a measure of how difficult it is to change the rotational speed of an object. Think of it as the rotational equivalent of mass in linear motion. A higher moment of inertia indicates a greater resistance to changes in angular velocity.
The moment of inertia (I) depends on both the mass distribution of the object and the axis of rotation. Mathematically, it's defined as the sum of the products of each particle's mass (dm) and the square of its distance (r) from the axis of rotation:
I = ∫ r² dm
This integral represents the summation over all infinitesimal mass elements within the object. The complexity of this integral depends heavily on the shape and mass distribution of the object.
Calculating the Moment of Inertia of a Quarter Circle
Calculating the moment of inertia of a quarter circle presents a slightly more challenging integration problem compared to simpler shapes like a solid disc or a rod. The challenge lies in the curved geometry and the need to express the infinitesimal mass (dm) in terms of the chosen coordinate system.
We'll consider two common scenarios:
-
Moment of inertia about an axis perpendicular to the plane of the quarter circle and passing through its center: This is often the most relevant scenario in practical applications.
-
Moment of inertia about an axis along one of the radii of the quarter circle: This scenario helps to illustrate the dependence of the moment of inertia on the axis of rotation.
Scenario 1: Moment of Inertia about the Center
Let's assume a homogeneous quarter circle with radius 'R' and mass 'M'. We'll use polar coordinates (r, θ) for ease of integration. The infinitesimal mass element (dm) can be expressed as:
dm = (M / (πR²/4)) * r dr dθ
Where:
- (M / (πR²/4)) is the mass density (mass per unit area) of the quarter circle.
- r dr dθ represents the infinitesimal area element in polar coordinates.
The distance (r) from the axis of rotation (perpendicular to the plane and passing through the center) is simply the radial coordinate 'r'. Therefore, the moment of inertia (I) becomes:
I = ∫∫ r² dm = ∫(θ=0 to π/2) ∫(r=0 to R) r² * (M / (πR²/4)) * r dr dθ
Solving this double integral yields:
I = (1/2)MR² - (4/π)MR²
After simplification and substitution, we get:
I = (1/2 - 4/π)MR² ≈ 0.1366 MR²
This is the moment of inertia of a quarter circle about an axis perpendicular to its plane and passing through its center. This is a crucial result with applications in various engineering disciplines, including mechanical design and structural analysis.
Scenario 2: Moment of Inertia about a Radius
Now let's consider the moment of inertia about an axis along one of the radii. This calculation requires a different approach. We'll still utilize polar coordinates, but the distance from the axis of rotation will change.
Let's choose the x-axis as the axis of rotation. In this case, the distance of an infinitesimal mass element from the x-axis is 'r sin θ'. Therefore, the moment of inertia (I_x) becomes:
I_x = ∫∫ (r sin θ)² dm = ∫(θ=0 to π/2) ∫(r=0 to R) (r² sin²θ) * (M / (πR²/4)) * r dr dθ
Solving this integral, we find:
I_x = (1/3)(MR²) - (4/π)(MR²/3)
After simplification, this simplifies to:
I_x = (1/3 - 4/(3π))MR² ≈ 0.1026 MR²
Notice that the moment of inertia about the radius is different from the moment of inertia about the center. This highlights the strong dependence of the moment of inertia on the chosen axis of rotation.
Parallel Axis Theorem
The parallel axis theorem offers a powerful shortcut for calculating the moment of inertia about an axis parallel to an axis passing through the object's center of mass. It states that the moment of inertia (I) about any axis parallel to and a distance 'd' from an axis through the center of mass (I_cm) is given by:
I = I_cm + Md²
Where 'M' is the object's mass.
This theorem can simplify calculations significantly when dealing with axes that aren't directly through the center of mass. For example, you could use the moment of inertia we calculated about the center of the quarter circle to calculate the moment of inertia about an axis parallel to the first one and some distance 'd' away.
Applications of Moment of Inertia of a Quarter Circle
The moment of inertia of a quarter circle finds applications in various engineering and physics problems:
-
Mechanical Design: Understanding the rotational inertia is vital for designing rotating machinery, such as gears, flywheels, and turbines. Accurate calculations ensure efficient operation and prevent catastrophic failures.
-
Structural Analysis: In structural engineering, calculating the moment of inertia is crucial for analyzing the bending and deflection of structures under load. This knowledge aids in designing robust and reliable structures.
-
Robotics: The moment of inertia plays a crucial role in designing robotic arms and manipulators. Accurate calculations ensure smooth, controlled movement and precise positioning.
-
Physics Simulations: In simulations involving rotating objects, knowing the moment of inertia is essential for generating accurate models of the object's behavior.
Conclusion
The calculation of the moment of inertia of a quarter circle, while more complex than some simpler shapes, is a fundamental problem in mechanics. Understanding the derivation, the different scenarios, and the applicability of theorems like the parallel axis theorem is crucial for professionals working in numerous fields. The result, whether about the center or a radius, serves as a foundational building block for more complex analyses and designs involving rotating bodies. The application of the moment of inertia extends far beyond the theoretical; its practical significance in engineering and physics is undeniable. Mastering this concept allows for accurate predictions of rotational behavior, efficient system design, and the development of robust and reliable structures.
Latest Posts
Latest Posts
-
Organelles That Are The Sites Of Protein Synthesis
Mar 31, 2025
-
What Is The Percentage Of 2 5
Mar 31, 2025
-
How To Find Reciprocal Of A Mixed Number
Mar 31, 2025
-
Which Of The Following Is Considered A Micronutrient
Mar 31, 2025
-
How Many Inches Is 2 Meters
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Moment Of Inertia Of Quarter Circle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
