How To Find Reciprocal Of A Mixed Number
Juapaving
Mar 31, 2025 · 5 min read
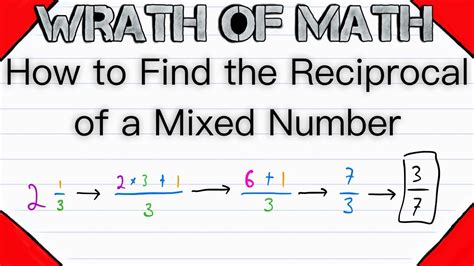
Table of Contents
How to Find the Reciprocal of a Mixed Number: A Comprehensive Guide
Finding the reciprocal of a mixed number might seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide breaks down the steps involved, providing practical examples and tips to master this essential mathematical concept. We'll explore why understanding reciprocals is crucial, delve into the definition, and provide numerous examples to solidify your understanding. By the end, you'll confidently calculate the reciprocal of any mixed number.
Understanding Reciprocals: The Foundation
Before diving into mixed numbers, let's establish a solid understanding of what a reciprocal is. Simply put, the reciprocal of a number is the number that, when multiplied by the original number, results in 1. This is also known as the multiplicative inverse.
For example:
- The reciprocal of 5 is 1/5 (because 5 * 1/5 = 1)
- The reciprocal of 1/3 is 3 (because 1/3 * 3 = 1)
- The reciprocal of 2/7 is 7/2 (because 2/7 * 7/2 = 1)
Notice a pattern? To find the reciprocal of a fraction, simply switch the numerator and the denominator.
Mixed Numbers: A Quick Refresher
A mixed number combines a whole number and a fraction. For instance, 2 ¾, 5 ⅓, and 1 1/2 are all mixed numbers. To work with mixed numbers effectively in the context of reciprocals, we need to convert them into improper fractions.
Converting Mixed Numbers to Improper Fractions
The process of converting a mixed number to an improper fraction involves three simple steps:
- Multiply the whole number by the denominator of the fraction: This gives you the total number of parts in the whole number portion.
- Add the numerator of the fraction to the result from step 1: This gives you the total number of parts in the entire mixed number.
- Keep the same denominator: The denominator remains unchanged throughout the process.
Let's illustrate this with an example: Convert 2 ¾ to an improper fraction.
- 2 (whole number) * 4 (denominator) = 8
- 8 + 3 (numerator) = 11
- The denominator remains 4.
Therefore, 2 ¾ is equivalent to the improper fraction 11/4.
Finding the Reciprocal of a Mixed Number: The Step-by-Step Process
Now that we can confidently convert mixed numbers to improper fractions, we can seamlessly find their reciprocals. Here's a step-by-step process:
- Convert the mixed number to an improper fraction: This is the crucial first step, as explained in the previous section.
- Switch the numerator and denominator of the improper fraction: This gives you the reciprocal.
Let's work through some examples:
Example 1: Find the reciprocal of 3 ⅔
-
Convert 3 ⅔ to an improper fraction:
- 3 * 3 = 9
- 9 + 2 = 11
- The denominator remains 3. So, 3 ⅔ = 11/3.
-
Find the reciprocal of 11/3:
- Switch the numerator and denominator: The reciprocal is 3/11.
Therefore, the reciprocal of 3 ⅔ is 3/11.
Example 2: Find the reciprocal of 1 ⅛
-
Convert 1 ⅛ to an improper fraction:
- 1 * 8 = 8
- 8 + 1 = 9
- The denominator remains 8. So, 1 ⅛ = 9/8.
-
Find the reciprocal of 9/8:
- Switch the numerator and denominator: The reciprocal is 8/9.
Therefore, the reciprocal of 1 ⅛ is 8/9.
Example 3: A more challenging example - Find the reciprocal of 7 ⁵⁄₁₂
-
Convert 7 ⁵⁄₁₂ to an improper fraction:
- 7 * 12 = 84
- 84 + 5 = 89
- The denominator remains 12. So, 7 ⁵⁄₁₂ = ⁸⁹⁄₁₂.
-
Find the reciprocal of ⁸⁹⁄₁₂:
- Switch the numerator and denominator: The reciprocal is ¹²/⁸⁹.
Therefore, the reciprocal of 7 ⁵⁄₁₂ is ¹²/⁸⁹.
Why Understanding Reciprocals is Important
Understanding reciprocals is fundamental to various mathematical operations and applications. Here are some key areas where this knowledge proves invaluable:
- Division of Fractions: Dividing by a fraction is equivalent to multiplying by its reciprocal. This simplifies complex division problems.
- Solving Equations: Reciprocals are essential in solving equations involving fractions and mixed numbers.
- Algebra: Reciprocals play a crucial role in algebraic manipulations and solving equations.
- Real-world Applications: Reciprocals are used in various fields, including physics, engineering, and finance, for calculations involving rates, ratios, and proportions.
Practicing to Master the Skill
The key to mastering the process of finding the reciprocal of a mixed number is consistent practice. Try working through these additional examples on your own:
- 4 ½
- 2 ⅓
- 5 ⁷⁄₁₀
- 1 ¹⁄₁₆
- 9 ⅘
Remember, the process always involves two key steps: converting the mixed number to an improper fraction, then switching the numerator and the denominator to find the reciprocal.
Troubleshooting Common Mistakes
While the process is relatively straightforward, some common mistakes can arise:
- Incorrect conversion to an improper fraction: Double-check your calculations when converting mixed numbers to improper fractions. A single error here will lead to an incorrect reciprocal.
- Forgetting to switch the numerator and denominator: Remember, the reciprocal involves switching the numerator and the denominator, not simply inverting the entire fraction.
- Working with improper fractions as mixed numbers: Ensure you consistently work with improper fractions throughout the process before calculating the reciprocal.
By carefully following each step and practicing regularly, you can avoid these mistakes and confidently find the reciprocal of any mixed number.
Conclusion: Embracing the Power of Reciprocals
Mastering the skill of finding the reciprocal of a mixed number is a significant step in improving your mathematical proficiency. It simplifies complex calculations, opens doors to more advanced mathematical concepts, and has practical applications across various fields. Remember the core steps: convert to an improper fraction, then switch the numerator and denominator. With consistent practice and attention to detail, you'll confidently navigate this essential mathematical concept.
Latest Posts
Latest Posts
-
What Is The Refractive Index Of A Vacuum
Apr 01, 2025
-
Predict The Product For The Following Reaction
Apr 01, 2025
-
What Is The Common Name Of Sodium Bicarbonate
Apr 01, 2025
-
Be Verb Forms V1 V2 V3 V4 V5
Apr 01, 2025
-
What Is The Multiple Of 23
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Find Reciprocal Of A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
