A Rectangle Is Sometimes A Square
Juapaving
Mar 31, 2025 · 5 min read
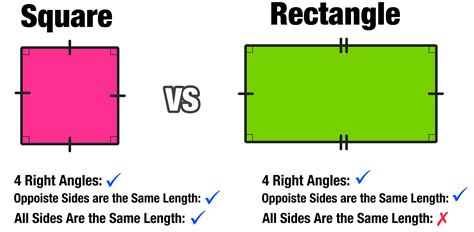
Table of Contents
A Rectangle is Sometimes a Square: Exploring the Nuances of Geometric Definitions
The seemingly simple statement, "a rectangle is sometimes a square," encapsulates a profound concept in geometry and logic: the relationship between inclusive and exclusive definitions. Understanding this relationship is crucial not only for mastering geometric principles but also for developing sharper analytical skills applicable across various fields. This article delves deep into the fascinating world of rectangles and squares, exploring their defining characteristics, uncovering the subtle yet significant differences, and ultimately demonstrating why a rectangle can indeed sometimes be a square.
Defining the Key Players: Rectangles and Squares
Before we dissect their relationship, let's establish clear definitions for our geometric protagonists.
What is a Rectangle?
A rectangle is a quadrilateral (a four-sided polygon) characterized by the following properties:
- Four right angles: Each of its interior angles measures exactly 90 degrees.
- Opposite sides are parallel and equal in length: This ensures the shape's symmetry and stability.
These two properties are sufficient to define a rectangle. No other conditions are necessary. A rectangle can be long and thin, short and wide, or even perfectly symmetrical.
What is a Square?
A square, on the other hand, is a more specific type of quadrilateral. It inherits all the properties of a rectangle but adds a crucial additional constraint:
- All four sides are equal in length: This condition introduces the concept of equilateral sides.
Therefore, a square possesses all the characteristics of a rectangle (four right angles, opposite sides parallel and equal) plus the extra condition of having all sides equal in length.
The Inclusive Nature of Geometric Definitions
The key to understanding why a rectangle can sometimes be a square lies in recognizing the inclusive nature of geometric definitions. Think of it as a hierarchy:
- Quadrilaterals: This is the broadest category, encompassing all four-sided shapes.
- Rectangles: A subset of quadrilaterals, possessing four right angles and opposite sides equal and parallel.
- Squares: A subset of rectangles, inheriting all rectangular properties and adding the constraint of equal side lengths.
This hierarchical structure illustrates that a square is a special case of a rectangle. It satisfies all the requirements to be classified as a rectangle, but it also meets an additional criterion that elevates it to the more specific category of a square.
This is analogous to other hierarchical classifications:
- All mammals are animals, but not all animals are mammals.
- All squares are rectangles, but not all rectangles are squares.
This inclusive definition is crucial. It doesn’t invalidate the unique characteristics of squares; instead, it correctly places them within the broader family of rectangles.
Visualizing the Relationship: Venn Diagrams and Set Theory
To further clarify the relationship between rectangles and squares, let's use a Venn diagram:
Imagine two circles. One represents all rectangles, and the other represents all squares. The circle representing squares is entirely contained within the circle representing rectangles. This visually demonstrates that every square is also a rectangle, but not every rectangle is a square.
This concept aligns perfectly with set theory. The set of all squares is a subset of the set of all rectangles. The relationship is one of inclusion, not exclusion.
Mathematical Representation and Proofs
We can further solidify this understanding through mathematical representations. Let's consider the following:
- Rectangular properties: Let the sides of a rectangle be denoted by a and b. The area is given by A = ab, and the perimeter is P = 2(a + b).
- Square properties: If we set a = b in the rectangular formulas, we obtain the formulas for a square: A = a², and P = 4a.
This mathematical representation clearly shows that the square’s formulas are simply a specialized case of the rectangle’s formulas, obtained by constraining the sides to be equal. This mathematical proof underscores the geometric relationship we've discussed.
Practical Applications and Real-World Examples
The distinction between rectangles and squares, and the understanding that a square is a special type of rectangle, has practical applications in various fields:
- Construction and Engineering: Designing buildings, bridges, and other structures often involves working with rectangles and squares. Understanding the properties of each shape is essential for ensuring stability and efficiency. A square foundation might be preferred in certain situations for its symmetry and strength.
- Computer Graphics and Programming: Representing shapes in computer programs often relies on understanding geometric definitions. The ability to identify a square as a specialized rectangle helps optimize algorithms and improve computational efficiency.
- Everyday Objects: Countless everyday objects exhibit rectangular and square shapes – books, windows, tiles, screens. Understanding the relationship between them allows for better organization, design, and spatial reasoning.
Addressing Common Misconceptions
A frequent misunderstanding arises from the belief that defining a square as a rectangle somehow diminishes the square’s uniqueness. This is incorrect. The inclusive nature of the definition simply recognizes the inherent relationship, enriching our understanding of geometry. The square retains its distinct properties; it’s merely also a member of a broader category.
Similarly, some might argue that this makes the concept of a square redundant. This is also inaccurate. The separate classification for squares is crucial for the clarity and precision required in mathematics and its applications. The term "square" allows for a more concise and accurate description when dealing with shapes with equal side lengths.
Conclusion: Embracing the Nuances of Geometric Relationships
The statement "a rectangle is sometimes a square" highlights a fundamental principle in mathematics: the power of inclusive definitions and the hierarchical relationships between different geometric shapes. Understanding this concept not only enhances our understanding of geometry but also sharpens our analytical and logical reasoning skills. A square remains unique with its equal sides, but its membership in the broader category of rectangles enriches our geometric understanding and provides a framework for more complex mathematical reasoning. By appreciating the nuances of these relationships, we unlock a deeper appreciation for the elegance and precision of mathematical concepts and their applications in the real world. The seemingly simple observation opens up a world of exploration into the intricacies of geometric definitions and their practical implications.
Latest Posts
Latest Posts
-
What Is The Lcm Of 5 And 10
Apr 02, 2025
-
Air Moves From High To Low Pressure
Apr 02, 2025
-
The Smallest Particle Of An Element Is A N
Apr 02, 2025
-
How Many Neutrons Does A Hydrogen Atom Have
Apr 02, 2025
-
What Is Nickel Used For In Everyday Life
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about A Rectangle Is Sometimes A Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
