Mass Moment Of Inertia For Rectangle
Juapaving
Mar 25, 2025 · 6 min read
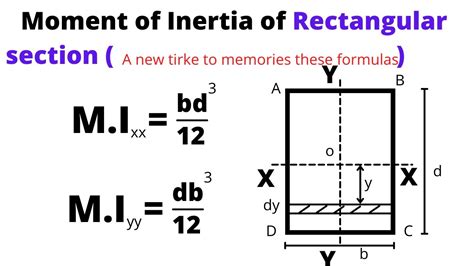
Table of Contents
Mass Moment of Inertia for a Rectangle: A Comprehensive Guide
The mass moment of inertia, often denoted as I, is a crucial concept in mechanics and engineering, representing an object's resistance to changes in its rotational motion. Understanding this property is vital for analyzing the dynamics of rotating systems, from simple pendulums to complex machinery. This comprehensive guide will delve into the calculation of the mass moment of inertia for a rectangle, covering various scenarios and providing practical applications.
Understanding Mass Moment of Inertia
Before diving into the specifics of rectangular shapes, let's establish a fundamental understanding of the mass moment of inertia. Unlike the moment of inertia in structural mechanics, which deals with resistance to bending, the mass moment of inertia describes the resistance to angular acceleration. Imagine trying to rotate a solid object; a heavier object or one with mass distributed further from the axis of rotation will be harder to accelerate. This resistance is quantified by the mass moment of inertia.
The mass moment of inertia depends on:
- Mass (m): A greater mass inherently resists changes in rotational motion more.
- Mass Distribution (r): The distribution of mass relative to the axis of rotation is crucial. Mass farther from the axis contributes more significantly to the moment of inertia.
- Axis of Rotation: The chosen axis significantly impacts the calculated value. The same object will have different moments of inertia about different axes.
Mathematically, the mass moment of inertia is calculated using integration:
I = ∫ r² dm
where:
- I is the mass moment of inertia
- r is the perpendicular distance from the infinitesimal mass element dm to the axis of rotation.
For simple shapes like rectangles, this integration can be simplified into readily usable formulas.
Mass Moment of Inertia of a Rectangle: Different Axes
The mass moment of inertia of a rectangle varies depending on the axis of rotation. We'll examine the most common scenarios:
1. Axis of Rotation through the Centroid, Parallel to a Side
Consider a rectangle with width b and height h, and uniform mass density ρ. The axis of rotation passes through the centroid (geometric center) and is parallel to one side (let's say the width b).
The formula for the mass moment of inertia in this case is:
I_x = (1/12) * m * h²
where:
- I_x is the mass moment of inertia about the x-axis (parallel to the width, through the centroid)
- m is the total mass of the rectangle (m = ρ * b * h)
- h is the height of the rectangle
Similarly, if the axis of rotation is parallel to the height h and passes through the centroid:
I_y = (1/12) * m * b²
where:
- I_y is the mass moment of inertia about the y-axis (parallel to the height, through the centroid)
- m is the total mass of the rectangle
- b is the width of the rectangle
Key takeaway: The moment of inertia is larger about the axis parallel to the longer side. This makes intuitive sense because more mass is located further from that axis.
2. Axis of Rotation through a Corner, Parallel to a Side
Now, let's consider an axis of rotation that passes through one corner of the rectangle and is parallel to one of the sides. This scenario requires a slightly different approach, employing the parallel axis theorem.
The Parallel Axis Theorem
The parallel axis theorem is a powerful tool that simplifies calculations when the axis of rotation is parallel to, but not through, the centroid. It states:
I = I_c + m * d²
where:
- I is the mass moment of inertia about the chosen axis
- I_c is the mass moment of inertia about a parallel axis through the centroid
- m is the mass of the object
- d is the distance between the two parallel axes
Applying this theorem to our corner case, where the axis is parallel to the width b and passes through a corner:
I_x' = I_x + m * (h/2)² = (1/12) * m * h² + m * (h/2)² = (1/3) * m * h²
Similarly, for an axis parallel to the height h and passing through a corner:
I_y' = I_y + m * (b/2)² = (1/12) * m * b² + m * (b/2)² = (1/3) * m * b²
Key takeaway: The moment of inertia increases significantly when the axis shifts from the centroid to a corner, reflecting the increased average distance of mass from the axis.
3. Axis of Rotation through the Centroid, Perpendicular to the Plane
This is the least intuitive scenario but nonetheless important. The axis of rotation is now perpendicular to the plane of the rectangle, passing through the centroid. This is often referred to as the polar moment of inertia, denoted J. It represents resistance to rotation about an axis perpendicular to the plane of the rectangle.
The formula is the sum of the moments of inertia about the x and y axes passing through the centroid:
J = I_x + I_y = (1/12) * m * (b² + h²)
Key takeaway: The polar moment of inertia combines the resistance to rotation about both in-plane axes, giving a comprehensive measure of rotational resistance about the axis perpendicular to the rectangle.
Practical Applications
Understanding the mass moment of inertia for rectangles has wide-ranging applications in various engineering fields:
-
Mechanical Design: Designing rotating components like gears, flywheels, and shafts requires accurate calculation of the mass moment of inertia to predict their dynamic behavior. This is critical for ensuring structural integrity and preventing failure under operational loads.
-
Robotics: Robotic manipulators consist of multiple links, often modeled as rectangular shapes. Accurately computing the moment of inertia of each link is fundamental to controlling the robot's movement, achieving precise positioning, and avoiding unwanted vibrations.
-
Aerospace Engineering: Aircraft wings and other components can be approximated as rectangular shapes, allowing for simplified calculations of the aircraft's moment of inertia, essential for flight dynamics simulations and control systems.
-
Civil Engineering: In structural analysis, the mass moment of inertia contributes to the understanding of torsional stiffness and vibration behavior of building elements.
-
Physics Simulations: Accurate moment of inertia calculations are essential for realistic simulations of physical systems involving rotation, like pendulums, gyroscopes, and other dynamic systems.
Beyond Simple Rectangles: Complex Shapes and Considerations
While the formulas above apply to homogeneous rectangles, real-world objects are rarely perfectly uniform. Let’s consider some complexities:
-
Non-uniform Density: If the density of the rectangle is not uniform (e.g., a composite material), the integration method becomes necessary. Numerical methods, such as finite element analysis, might be needed for precise calculations.
-
Complex Shapes: For shapes that are not simple rectangles (e.g., L-shaped profiles, irregular polygons), the calculation becomes more involved. Techniques like dividing the shape into smaller, simpler rectangular elements and summing their individual moments of inertia can be employed, or more advanced methods like numerical integration might be necessary.
-
Composite Bodies: Many systems consist of multiple interconnected parts. The total moment of inertia of such a composite body is determined by summing the moments of inertia of individual components, taking into account their respective masses and positions.
Conclusion
The mass moment of inertia for a rectangle is a fundamental concept in mechanics with significant implications in various engineering disciplines. Understanding the formulas for different axes of rotation and the parallel axis theorem is crucial for accurate analysis and design. While simple rectangular shapes offer readily available formulas, complex shapes and non-uniform densities may require more advanced computational techniques. Mastering these concepts is essential for any engineer or physicist working with rotating systems. Remember to always carefully consider the axis of rotation and the mass distribution when calculating the mass moment of inertia. The accuracy of your calculations directly impacts the reliability and performance of the system you're analyzing or designing.
Latest Posts
Latest Posts
-
Which Expression Is Equivalent To Sqrt 200
Mar 28, 2025
-
Is N More Electronegative Than C
Mar 28, 2025
-
Lcm Of 3 7 And 10
Mar 28, 2025
-
A Tuning Fork Of Frequency 440 Hz
Mar 28, 2025
-
Are Non Metals Good Conductors Of Electricity
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Mass Moment Of Inertia For Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
