Magnetic Field From A Current Loop
Juapaving
Apr 02, 2025 · 7 min read
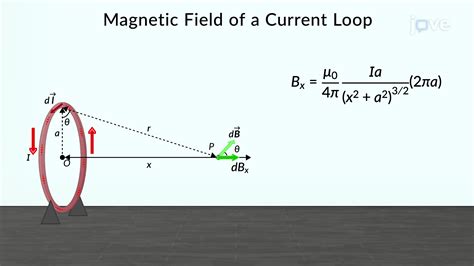
Table of Contents
Magnetic Field from a Current Loop: A Comprehensive Guide
The magnetic field generated by a current loop is a fundamental concept in electromagnetism with wide-ranging applications in various fields, from electric motors and generators to scientific instruments and medical technology. Understanding this field is crucial for comprehending the principles behind many technologies we use daily. This comprehensive guide delves deep into the magnetic field produced by a current loop, exploring its characteristics, calculations, and practical implications.
Understanding the Basics: Current, Loops, and Magnetic Fields
Before diving into the complexities of the magnetic field from a current loop, let's establish a firm grasp of the fundamental concepts:
Current: The Flow of Charge
Electric current is the flow of electric charge. In most practical scenarios, this charge is carried by electrons moving through a conductor, like a wire. The magnitude of the current is measured in Amperes (A), representing the rate of charge flow. A higher current indicates a greater flow of charge per unit time.
Loops: Shaping the Magnetic Field
When a current flows through a straight wire, it generates a circular magnetic field around the wire. The direction of this field can be determined using the right-hand rule: if you point your thumb in the direction of the current, your fingers curl in the direction of the magnetic field lines.
Creating a loop, however, significantly alters the magnetic field's configuration. By bending the wire into a closed loop, we concentrate the magnetic field within and around the loop, resulting in a much stronger and more focused field.
Magnetic Field: A Force Field
A magnetic field is a vector field, meaning it has both magnitude and direction at each point in space. It exerts a force on moving charged particles and magnetic materials. The strength of the magnetic field is measured in Teslas (T). Magnetic field lines are used to visualize the field; they indicate the direction of the force a north magnetic pole would experience if placed in the field.
Calculating the Magnetic Field: Biot-Savart Law and its Application
The Biot-Savart Law provides a powerful tool for calculating the magnetic field produced by a current-carrying wire of any shape. For a small segment of wire, the law states that the magnetic field dB is proportional to the current I, the length of the segment dl, and inversely proportional to the square of the distance r from the segment. The direction of dB is perpendicular to both dl and r. Mathematically, this is expressed as:
dB = (μ₀/4π) * (I * dl x r) / r³
where:
- dB: The magnetic field contribution from a small segment of the wire
- μ₀: The permeability of free space (a constant)
- I: The current flowing through the wire
- dl: A small vector element along the wire, pointing in the direction of the current
- r: The vector pointing from the wire segment to the point where the magnetic field is being calculated
- x: Represents the cross product, which gives a vector perpendicular to both dl and r
For a circular loop of radius 'a', calculating the total magnetic field at a point along the axis of symmetry involves integrating the Biot-Savart law over the entire loop. This integration is more complex and yields the following formula for the magnetic field B at a distance z from the center of the loop along its axis:
B = (μ₀ * I * a²) / (2 * (a² + z²)^(3/2))
This equation shows that the magnetic field strength along the axis of the loop depends on the current I, the loop's radius a, and the distance z from the center. The field is strongest at the center of the loop (z=0) and weakens as you move further away along the axis.
Exploring the Field: Key Characteristics and Patterns
Several key characteristics define the magnetic field generated by a current loop:
Axial Symmetry: A Consistent Pattern
The magnetic field of a current loop exhibits axial symmetry. This means the field is symmetrical about the axis passing through the center of the loop and perpendicular to its plane. The field lines are closed loops that encircle the current-carrying wire.
Field Strength and Distance: An Inverse Relationship
The strength of the magnetic field decreases as the distance from the loop increases. This inverse relationship is evident in the formula derived from the Biot-Savart Law. The field weakens more rapidly along the axis than in the plane of the loop.
Field Direction: The Right-Hand Rule Revisited
The direction of the magnetic field can be determined using the right-hand rule. Curl your fingers in the direction of the current flow in the loop; your thumb will point in the direction of the magnetic field at the center of the loop. Outside the loop, the field lines resemble those of a bar magnet.
Magnetic Dipole Moment: A Key Property
A current loop acts as a magnetic dipole, possessing a magnetic dipole moment (µ). This moment is a vector quantity, given by:
µ = I * A
where:
- µ: The magnetic dipole moment
- I: The current in the loop
- A: The area enclosed by the loop
The magnetic dipole moment is a measure of the loop's strength as a magnetic source. A larger current or loop area results in a stronger magnetic dipole moment. This concept is crucial for understanding the interaction of current loops with external magnetic fields.
Applications of Magnetic Fields from Current Loops: From Motors to Medical Devices
The magnetic field produced by a current loop is fundamental to numerous technologies and applications. Here are some notable examples:
Electric Motors and Generators: Harnessing Magnetic Forces
Electric motors and generators rely on the interaction between magnetic fields and current-carrying conductors. In a motor, the magnetic field generated by a current loop (often a coil of wire) interacts with a permanent magnet or another electromagnet, creating a torque that causes rotation. In a generator, the rotation of a coil within a magnetic field induces a current.
Loudspeakers: Transforming Electrical Signals into Sound Waves
Loudspeakers use electromagnetism to convert electrical signals into sound waves. A current-carrying coil placed in the magnetic field of a permanent magnet experiences a force proportional to the current. This force moves the coil, which in turn vibrates a diaphragm, producing sound.
Magnetic Resonance Imaging (MRI): Medical Imaging through Magnetic Fields
MRI utilizes powerful magnetic fields generated by superconducting electromagnets (which are essentially very large current loops) to create detailed images of the internal structures of the body. These magnetic fields interact with the atomic nuclei in the body, generating signals that are processed to form images.
Scientific Instruments: Precision Measurement and Control
Many scientific instruments utilize the magnetic field from current loops for precision measurement and control. For example, they are employed in devices used to measure magnetic susceptibility, current, and other physical quantities.
Beyond the Basics: Exploring More Complex Scenarios
While the simple circular loop provides a fundamental understanding, many real-world applications involve more complex configurations. These include:
Solenoids: Concentrating the Magnetic Field
A solenoid is a coil of wire wound in a tight helix. The magnetic field within a long solenoid is remarkably uniform and strong, making them ideal for applications where a consistent magnetic field is required. The field strength within the solenoid is given approximately by:
B = μ₀ * n * I
where:
- n: The number of turns of wire per unit length
Helmholtz Coils: Creating a Homogeneous Field
Two identical coaxial current loops placed a distance apart create a nearly uniform magnetic field in the region between them. These are known as Helmholtz coils and are used to create precisely controlled magnetic fields for various experiments and applications.
Toroids: Shaping the Magnetic Field for Specific Applications
A toroid is a coil of wire wound around a doughnut-shaped core. The magnetic field within the toroid is largely confined to the core, making them useful for applications where magnetic field leakage needs to be minimized.
Conclusion: A Foundation for Understanding Electromagnetism
The magnetic field from a current loop is a cornerstone of electromagnetism, underpinning numerous technologies and applications. Understanding the principles governing this field, from the Biot-Savart Law to the behavior of solenoids and other coil configurations, is essential for anyone seeking a deeper appreciation of how electromagnetism shapes our world. This guide provides a comprehensive foundation for further exploration into this fascinating and vital area of physics. Further research into specific applications and more advanced calculations will expand your understanding of this powerful phenomenon.
Latest Posts
Latest Posts
-
Do Metals Lose Or Gain Electrons
Apr 03, 2025
-
How Many Electrons Are In Phosphorus
Apr 03, 2025
-
Common Multiples Of 5 And 2
Apr 03, 2025
-
Choose The True Statement About The Krebs Cycle
Apr 03, 2025
-
Essay On The Pleasure Of Reading
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Magnetic Field From A Current Loop . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
