Lines Of Symmetry For A Hexagon
Juapaving
Apr 06, 2025 · 5 min read
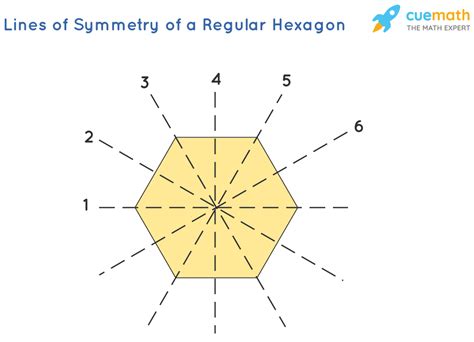
Table of Contents
Lines of Symmetry for a Hexagon: A Comprehensive Guide
Symmetry, a captivating concept in geometry, refers to the balanced proportions of a figure. Understanding lines of symmetry is crucial for grasping the fundamental properties of shapes, and the hexagon, with its six sides and angles, provides an excellent case study. This article delves deep into the world of hexagonal symmetry, exploring different types of hexagons and meticulously detailing their lines of symmetry. We'll unravel the mathematical principles behind these lines, illustrating concepts with clear examples and diagrams. By the end, you’ll have a thorough understanding of symmetry in hexagons, regardless of your prior mathematical experience.
What is a Line of Symmetry?
Before diving into the specifics of hexagons, let’s establish a clear understanding of what a line of symmetry actually is. A line of symmetry, also known as a line of reflection or axis of symmetry, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, both halves would perfectly overlap. This implies that every point on one side of the line has a corresponding point on the other side, equidistant from the line of symmetry.
Types of Hexagons and their Symmetry
Not all hexagons are created equal. The number of lines of symmetry a hexagon possesses depends heavily on its shape and properties. Let's explore the key types:
1. Regular Hexagon: The Perfect Symmetry
A regular hexagon is defined by its six equal sides and six equal angles (each measuring 120 degrees). This perfectly symmetrical shape boasts a remarkable six lines of symmetry. These lines can be categorized into two groups:
-
Three lines of symmetry connecting opposite vertices: These lines run directly from one vertex (corner) to the opposite vertex. Imagine drawing a line from one corner to the opposite corner; this line divides the hexagon perfectly in half. There are three such lines in a regular hexagon.
-
Three lines of symmetry bisecting opposite sides: These lines run perpendicularly to pairs of opposite sides, dividing each side into two equal segments. Again, folding the hexagon along any of these lines would result in perfect overlap.
(Insert a diagram here showcasing a regular hexagon with its six lines of symmetry clearly marked and labeled.)
2. Irregular Hexagons: A Spectrum of Symmetry
Irregular hexagons, unlike their regular counterparts, lack equal sides and angles. The number of lines of symmetry in an irregular hexagon can vary greatly, ranging from zero to a maximum of three, depending on the specific arrangement of its sides and angles. It's crucial to understand that even slight deviations from the regular hexagon's perfect form can drastically reduce or eliminate its lines of symmetry.
Consider these scenarios:
-
Zero lines of symmetry: A completely irregular hexagon, with all its sides and angles differing significantly, will possess no lines of symmetry.
-
One line of symmetry: An irregular hexagon might have one line of symmetry if it exhibits a certain degree of bilateral symmetry – meaning it can be divided into two mirror-image halves by a single line.
-
Two lines of symmetry: It's possible for an irregular hexagon to have two lines of symmetry, although this is less common than one or zero.
-
Three lines of symmetry: This scenario is possible, but only under specific conditions of irregular shapes exhibiting certain proportional balances.
(Insert multiple diagrams here illustrating irregular hexagons with zero, one, two, and three lines of symmetry respectively. Clearly label each diagram to emphasize the number of lines of symmetry.)
Mathematical Proof of Lines of Symmetry in a Regular Hexagon
The existence of six lines of symmetry in a regular hexagon can be proven mathematically. The proof leverages the rotational symmetry of the hexagon and the concept of reflection.
A regular hexagon has rotational symmetry of order 6. This means it can be rotated about its center by multiples of 60 degrees (360°/6 = 60°) and still look identical. Each of these six rotational positions corresponds to a line of symmetry. By drawing lines connecting the center of the hexagon to each vertex, we can observe that these lines bisect the opposite sides, resulting in three lines of symmetry. Additionally, lines connecting opposite vertices also create three lines of symmetry.
This mathematical foundation solidifies the six lines of symmetry characteristic of a regular hexagon.
Applications of Hexagonal Symmetry
The understanding of hexagonal symmetry has practical applications in various fields:
-
Nature: Honeycombs, a marvel of natural engineering, perfectly demonstrate hexagonal symmetry. Bees instinctively construct hexagonal cells to maximize space and efficiency in storing honey. Similarly, the structure of snowflakes often reflects hexagonal symmetry.
-
Engineering and Design: Hexagonal patterns are frequently used in engineering and design for their strength and stability. Hexagonal tiles are commonly used in flooring and paving due to their ability to tessellate perfectly, covering a surface without gaps.
-
Art and Architecture: The aesthetically pleasing symmetry of hexagons is often exploited in art and architecture. Many artistic designs and architectural structures incorporate hexagonal patterns to achieve a visually balanced and pleasing effect.
Exploring Further: Symmetry in Other Polygons
Understanding hexagonal symmetry can be a springboard to exploring symmetry in other polygons. The number of lines of symmetry in a regular polygon is directly related to the number of its sides. A regular polygon with 'n' sides has 'n' lines of symmetry if 'n' is odd, and 'n' lines of symmetry plus 'n'/2 lines connecting opposite vertices if 'n' is even.
This knowledge empowers you to analyze and predict the symmetry of various geometric shapes, broadening your understanding of geometric principles.
Conclusion: The Elegance of Hexagonal Symmetry
Hexagonal symmetry, particularly in the case of the regular hexagon, is a beautiful and powerful concept. The six lines of symmetry demonstrate the perfect balance and harmony inherent in this geometric shape. This article aimed to demystify the concept of hexagonal symmetry, providing both a conceptual and mathematical understanding. By exploring different types of hexagons and their varying symmetry levels, we've unveiled the elegance and importance of this fundamental geometric principle in both the natural world and human creations. Further exploration into symmetry in other polygons builds upon this foundation, enriching your comprehension of geometrical properties and their diverse applications.
Latest Posts
Latest Posts
-
What Is The Electronic Configuration Of Calcium
Apr 07, 2025
-
Why Is Blood Regarded As A Connective Tissue
Apr 07, 2025
-
Prime Implicants And Essential Prime Implicants
Apr 07, 2025
-
How Tall Is 49 Inches In Feet
Apr 07, 2025
-
The Ratio Between Map Distance And Ground Distance Is Called
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Lines Of Symmetry For A Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.