Least Common Multiple Of 25 And 15
Juapaving
Mar 26, 2025 · 5 min read
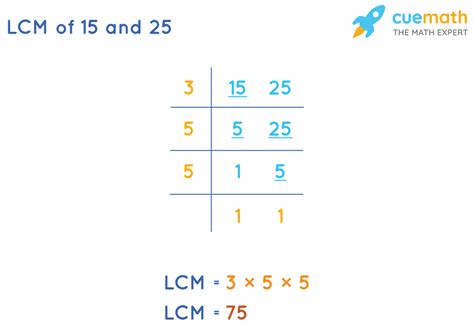
Table of Contents
Unveiling the Least Common Multiple (LCM) of 25 and 15: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods for calculation opens up a fascinating world of number theory. This article will delve into the LCM of 25 and 15, explaining not just the answer but the why behind the process, exploring various methods, and demonstrating the broader applications of LCM in mathematics and beyond.
What is a Least Common Multiple (LCM)?
Before we tackle the specific case of 25 and 15, let's solidify our understanding of LCM. The LCM of two or more integers is the smallest positive integer that is a multiple of all the numbers. Think of it as the smallest number that can be divided evenly by all the given numbers without leaving a remainder.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24, 28... and the multiples of 6 are 6, 12, 18, 24, 30... Notice that 12 and 24 appear in both lists. The smallest of these common multiples is 12, therefore, the LCM of 4 and 6 is 12.
Method 1: Listing Multiples
This is the most straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 25: 25, 50, 75, 100, 125, 150, 175...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165...
By comparing the two lists, we observe that the smallest common multiple is 75. Therefore, the LCM(25, 15) = 75.
Method 2: Prime Factorization
This method is more efficient for larger numbers and offers a deeper understanding of the underlying mathematical principles. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
-
Find the prime factorization of each number:
- 25 = 5 x 5 = 5²
- 15 = 3 x 5
-
Identify the highest power of each prime factor:
- The prime factors are 3 and 5.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5².
-
Multiply the highest powers together:
- LCM(25, 15) = 3¹ x 5² = 3 x 25 = 75
This method elegantly reveals the structure of the LCM, highlighting the role of prime factors.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are intimately related. There's a handy formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 25 and 15. We can use the Euclidean algorithm for this:
- Divide the larger number (25) by the smaller number (15): 25 ÷ 15 = 1 with a remainder of 10.
- Replace the larger number with the smaller number (15) and the smaller number with the remainder (10): 15 ÷ 10 = 1 with a remainder of 5.
- Repeat: 10 ÷ 5 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 5.
Now, we can use the formula:
LCM(25, 15) x GCD(25, 15) = 25 x 15 LCM(25, 15) x 5 = 375 LCM(25, 15) = 375 ÷ 5 = 75
Applications of LCM in Real-World Scenarios
While finding the LCM of 25 and 15 might seem purely academic, the concept has numerous practical applications:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 25 minutes, and the other every 15 minutes. The LCM (75 minutes) tells us when both buses will arrive at the stop simultaneously again.
-
Project Management: If different tasks in a project require 25 and 15 units of time respectively, the LCM helps determine the shortest time frame to complete both tasks if they're performed in a cyclical manner.
-
Music: Musical rhythms and harmonies often rely on LCM to determine the least common multiple of different note lengths or beat frequencies, ensuring a coherent and rhythmic sound.
-
Gear Ratios: In mechanical engineering, gear ratios are designed using the concept of LCM to ensure smooth and efficient power transmission. A given gear arrangement will synchronize after the time represented by the LCM of the individual gears' rotation periods.
-
Calendars: The LCM is used in calculating the period after which certain calendar events (like the overlap of specific days of the week and months) will occur again.
Beyond the Basics: Extending the Concept
The LCM isn't limited to just two numbers. We can find the LCM of any number of integers using the prime factorization method. For example, to find the LCM of 10, 15, and 20:
-
Prime factorization:
- 10 = 2 x 5
- 15 = 3 x 5
- 20 = 2² x 5
-
Highest powers:
- 2²
- 3¹
- 5¹
-
Multiply: LCM(10, 15, 20) = 2² x 3 x 5 = 60
Conclusion:
The seemingly simple task of finding the least common multiple of 25 and 15 reveals a wealth of mathematical concepts and practical applications. Understanding different methods for calculating the LCM, such as listing multiples, prime factorization, and using the GCD, provides valuable tools for problem-solving in various fields. Whether it's scheduling, music composition, or engineering design, the LCM plays a crucial role in ensuring efficiency and synchronization. The exploration of LCM goes beyond basic arithmetic, offering insights into the fundamental building blocks of number theory and showcasing its relevance in the real world. Mastering this concept enhances your mathematical toolkit and provides a solid foundation for tackling more complex mathematical problems.
Latest Posts
Latest Posts
-
How Many Hearts Does Wormsn Have
Mar 29, 2025
-
Write The Prime Factorization Of 75
Mar 29, 2025
-
What Is The Lcm Of 14 And 12
Mar 29, 2025
-
Find The Greatest Common Factor Of 12 And 18
Mar 29, 2025
-
Which Graph Represents An Odd Function
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 25 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
