Write The Prime Factorization Of 75
Juapaving
Mar 29, 2025 · 5 min read
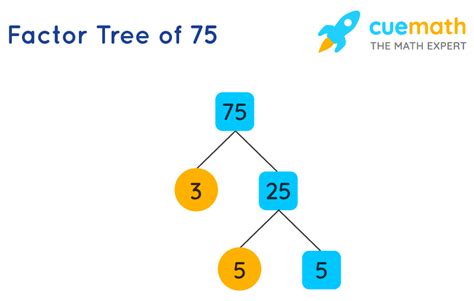
Table of Contents
Prime Factorization of 75: A Deep Dive into Number Theory
The seemingly simple question, "What is the prime factorization of 75?" opens a door to a fascinating world of number theory. While the answer itself is relatively straightforward, exploring the process and the underlying concepts provides a solid foundation for understanding more complex mathematical principles. This article will not only answer the question but delve into the significance of prime factorization, its applications, and related mathematical concepts.
Understanding Prime Numbers and Prime Factorization
Before we tackle the prime factorization of 75, let's define the key terms:
-
Prime Number: A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. These are the fundamental building blocks of all other whole numbers.
-
Prime Factorization: Prime factorization (or prime decomposition) is the process of expressing a composite number (a number greater than 1 that is not prime) as a product of its prime factors. This representation is unique for every composite number. In other words, every composite number can be broken down into a unique set of prime numbers multiplied together.
Finding the Prime Factorization of 75
Now, let's find the prime factorization of 75. We can use a method called the factor tree.
-
Start with the number: Begin with the number 75.
-
Find a pair of factors: We can start by finding any two numbers that multiply to give 75. A simple choice is 3 and 25. We write these as branches from 75.
-
Continue factoring: Now we look at each branch. 3 is a prime number, so we circle it. 25 is not prime (it's divisible by 5), so we further factor it into 5 and 5.
-
Identify the prime factors: We now have the prime factors: 3, 5, and 5.
Therefore, the prime factorization of 75 is 3 x 5 x 5, which can also be written as 3 x 5<sup>2</sup>.
This is a unique representation. No other combination of prime numbers will multiply to give 75. This uniqueness is a cornerstone of number theory.
The Significance of Prime Factorization
Prime factorization is more than just a mathematical exercise; it has significant implications across various fields:
1. Cryptography:
Prime numbers and factorization play a crucial role in modern cryptography. Many encryption algorithms rely on the difficulty of factoring very large numbers into their prime factors. The security of these systems depends on the computational infeasibility of factoring these numbers, even with powerful computers. RSA encryption, one of the most widely used public-key cryptosystems, hinges on this principle.
2. Number Theory:
Prime factorization is fundamental to many areas of number theory. It underpins concepts like the greatest common divisor (GCD) and the least common multiple (LCM), which are crucial for simplifying fractions and solving various mathematical problems. Understanding prime factorization provides a deep understanding of the structure and relationships between whole numbers.
3. Computer Science:
Prime factorization algorithms are an active area of research in computer science. Developing efficient algorithms to factor large numbers is a significant challenge with potential implications for breaking cryptographic systems. These algorithms are used in various applications, including database indexing and optimization.
4. Modular Arithmetic:
Modular arithmetic, where numbers "wrap around" after reaching a certain value (the modulus), heavily uses prime numbers and prime factorization. This system is employed in numerous applications, from cryptography to computer programming.
Exploring Related Concepts
Several related mathematical concepts build upon the foundation of prime factorization:
1. Greatest Common Divisor (GCD):
The GCD of two or more numbers is the largest number that divides each of them without leaving a remainder. Finding the GCD can be greatly simplified by using the prime factorization of the numbers. For example, to find the GCD of 75 and 105, we first find their prime factorizations:
- 75 = 3 x 5<sup>2</sup>
- 105 = 3 x 5 x 7
The common prime factors are 3 and 5. Therefore, the GCD(75, 105) = 3 x 5 = 15.
2. Least Common Multiple (LCM):
The LCM of two or more numbers is the smallest number that is a multiple of each of them. Similar to the GCD, the LCM can also be efficiently calculated using prime factorization. Using the same example:
- 75 = 3 x 5<sup>2</sup>
- 105 = 3 x 5 x 7
To find the LCM, we take the highest power of each prime factor present in either factorization: 3<sup>1</sup>, 5<sup>2</sup>, and 7<sup>1</sup>. Therefore, the LCM(75, 105) = 3 x 5<sup>2</sup> x 7 = 525.
3. Unique Prime Factorization Theorem (Fundamental Theorem of Arithmetic):
This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This theorem is the cornerstone of many number theoretic concepts. The unique prime factorization of 75, 3 x 5<sup>2</sup>, is an example of this theorem in action.
Advanced Topics and Further Exploration
The world of prime numbers and prime factorization extends far beyond the basic concepts discussed above. Advanced topics include:
-
The Riemann Hypothesis: This unsolved problem in mathematics concerns the distribution of prime numbers and has profound implications for number theory.
-
Prime Number Theorem: This theorem provides an approximate formula for the number of primes less than a given number.
-
Mersenne Primes: These are prime numbers that are one less than a power of two. Finding large Mersenne primes is an active area of research.
-
Twin Primes: These are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). The twin prime conjecture, which posits that there are infinitely many twin primes, remains an unsolved problem.
Conclusion
The seemingly simple question of the prime factorization of 75 unveils a rich tapestry of mathematical concepts and applications. From cryptography to computer science and number theory, understanding prime factorization is essential for tackling complex problems and driving innovation across various fields. While the factorization of 75 itself is easily calculated, the underlying principles and their broader implications highlight the profound importance of prime numbers in the world of mathematics and beyond. Further exploration of these concepts will undoubtedly enrich your understanding of the fundamental building blocks of numbers and the elegant structures they form.
Latest Posts
Latest Posts
-
Is Oxygen A Metal Nonmetal Or Metalloid
Mar 31, 2025
-
Keyboard Is A Hardware Or Software
Mar 31, 2025
-
Is 45 A Multiple Of 9
Mar 31, 2025
-
Forward Primer And Reverse Primer In Pcr
Mar 31, 2025
-
Words That Begin With A H
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Write The Prime Factorization Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
