Least Common Factor Of 8 And 9
Juapaving
Mar 26, 2025 · 6 min read
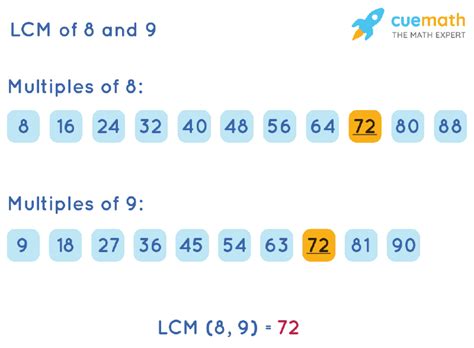
Table of Contents
Finding the Least Common Factor (LCM) of 8 and 9: A Comprehensive Guide
The concept of the Least Common Multiple (LCM), often confused with the Greatest Common Factor (GCF), is a fundamental aspect of number theory with widespread applications in mathematics, computer science, and even everyday life. This article dives deep into understanding the LCM, specifically focusing on finding the LCM of 8 and 9. We'll explore various methods, discuss the underlying principles, and illustrate the practical relevance of this seemingly simple calculation.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This is different from the Greatest Common Factor (GCF), which is the largest number that divides evenly into all the given numbers. Understanding the difference between LCM and GCF is crucial for accurate calculations.
Methods for Finding the LCM of 8 and 9
There are several effective methods for determining the LCM of two numbers, and we'll explore three common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple that is common to both.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
By comparing the lists, we find that the smallest common multiple is 72. Therefore, the LCM(8, 9) = 72. This method is simple to understand but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM from these prime factors.
- Prime factorization of 8: 2³ (8 = 2 x 2 x 2)
- Prime factorization of 9: 3² (9 = 3 x 3)
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
Multiplying these highest powers together gives us the LCM: 8 x 9 = 72. Therefore, the LCM(8, 9) = 72. This method is more systematic and less prone to errors than the listing method, especially when dealing with larger numbers or more than two numbers.
3. Formula Method using GCF
This method leverages the relationship between the LCM and the GCF (Greatest Common Factor). The formula is:
LCM(a, b) = (a x b) / GCF(a, b)
First, we need to find the GCF of 8 and 9. The GCF is the greatest number that divides both 8 and 9 without leaving a remainder. In this case, the only common factor of 8 and 9 is 1. Therefore, GCF(8, 9) = 1.
Now, we can apply the formula:
LCM(8, 9) = (8 x 9) / 1 = 72
This confirms that the LCM of 8 and 9 is indeed 72. This method is efficient once the GCF is known, and finding the GCF is often relatively straightforward, especially for smaller numbers.
Why is Finding the LCM Important?
The LCM has numerous practical applications across various fields:
-
Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/8 and 1/9, we need to find the LCM of 8 and 9 (which is 72), then express each fraction with a denominator of 72 before adding them.
-
Scheduling: Imagine you have two tasks that repeat at different intervals. One task repeats every 8 days, and another every 9 days. To find when both tasks will occur on the same day again, you need to find the LCM of 8 and 9. The LCM of 8 and 9 is 72, so both tasks will coincide every 72 days.
-
Modular Arithmetic: In computer science and cryptography, LCM plays a crucial role in modular arithmetic, which is used in various algorithms and security protocols.
-
Geometry: LCM is used in solving problems related to finding the least common length or area, especially when dealing with shapes with different dimensions.
Extending the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply incorporate all prime factors from all the numbers, taking the highest power of each prime factor. For the formula method, you would need to find the GCF of all the numbers, which can be a bit more complex but is still a manageable process.
Practical Applications and Real-World Examples
Let’s consider some real-world scenarios where understanding LCM proves valuable:
Scenario 1: Concert Scheduling
Two bands are scheduled to perform at a festival. Band A performs every 8 days, and Band B performs every 9 days. When will both bands perform on the same day?
The solution involves finding the LCM(8, 9) = 72. Both bands will perform on the same day every 72 days.
Scenario 2: Packaging Products
A company manufactures two types of products, packaged in boxes of 8 and 9 units respectively. What is the smallest number of boxes needed to have an equal number of both products?
This problem requires finding the LCM(8, 9) = 72. The company needs to order 9 boxes of the first product and 8 boxes of the second product to have 72 units of each.
Scenario 3: Cycling Intervals
Two cyclists start cycling around a circular track. One cyclist completes a lap every 8 minutes, and the other every 9 minutes. After how many minutes will they be at the starting point simultaneously again?
This is equivalent to finding the LCM(8, 9) = 72 minutes.
Conclusion
Understanding and calculating the LCM is a fundamental skill with diverse applications in various aspects of life. Whether dealing with fractions, scheduling events, or solving problems in geometry, the LCM provides an essential tool for efficient and accurate solutions. The methods explored in this article, particularly the prime factorization method, equip individuals with the ability to tackle LCM calculations confidently, regardless of the complexity of the numbers involved. Mastering LCM calculations enhances mathematical proficiency and opens doors to a more profound understanding of numerical relationships. Remember to choose the method best suited to the numbers you're working with – the listing method for small numbers, and prime factorization or the formula method for larger numbers or more complex scenarios.
Latest Posts
Latest Posts
-
What Is Depicted In The Image Above
Mar 29, 2025
-
14 Meters Is How Many Feet
Mar 29, 2025
-
How Many Electrons In Oxygen Atom
Mar 29, 2025
-
Whats The Prime Factorization Of 15
Mar 29, 2025
-
37 Inches Is How Many Feet
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Least Common Factor Of 8 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
