Least Common Factor Of 7 And 9
Juapaving
Mar 29, 2025 · 5 min read
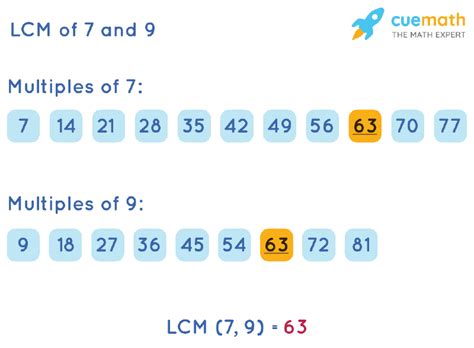
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 9: A Comprehensive Guide
The concept of Least Common Multiple (LCM) is a fundamental element in number theory and has widespread applications in various fields, from scheduling problems to simplifying fractions. This comprehensive guide will delve into the process of finding the LCM of 7 and 9, exploring different methods and providing a thorough understanding of the underlying principles. We will also discuss the relationship between LCM and the Greatest Common Divisor (GCD), a crucial concept often intertwined with LCM calculations.
Understanding Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that can be divided evenly by each of the given numbers without leaving a remainder. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Why is LCM Important?
LCM finds its utility in numerous real-world applications:
- Scheduling: Determining when events will occur simultaneously. For example, if two buses leave a station at different intervals, the LCM helps find when they will depart at the same time again.
- Fraction Operations: Finding a common denominator when adding or subtracting fractions. This simplifies the calculation and ensures accuracy.
- Modular Arithmetic: Solving problems involving remainders and congruences.
- Pattern Recognition: Identifying repeating patterns in sequences.
- Music Theory: Calculating the rhythmic relationships between notes.
Methods for Finding the LCM of 7 and 9
Several methods can be used to determine the LCM of 7 and 9. Let's explore the most common and effective approaches:
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, ...
By comparing the lists, we observe that the smallest common multiple is 63.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3² (9 = 3 x 3)
Since 7 and 3 are different prime numbers, the LCM is simply the product of their highest powers: 7 x 3² = 7 x 9 = 63.
3. Formula Using GCD (Greatest Common Divisor)
The LCM and GCD of two numbers are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This relationship provides an alternative method for finding the LCM.
First, we need to find the GCD of 7 and 9. Since 7 and 9 share no common factors other than 1, their GCD is 1.
Using the formula: LCM(a, b) = (a x b) / GCD(a, b)
LCM(7, 9) = (7 x 9) / 1 = 63
This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more time-consuming.
Why 63 is the LCM of 7 and 9: A Deeper Dive
The LCM, 63, represents the smallest number that is perfectly divisible by both 7 and 9. This means that:
- 63 ÷ 7 = 9 (with no remainder)
- 63 ÷ 9 = 7 (with no remainder)
No smaller positive integer satisfies both conditions. Any other common multiple of 7 and 9 will be a multiple of 63 (e.g., 126, 189, etc.).
Applications of LCM in Real-World Scenarios
Let's explore some real-world scenarios demonstrating the practical application of the LCM:
1. Scheduling Train Departures:
Imagine two trains departing from a station. Train A departs every 7 minutes, and Train B departs every 9 minutes. To find out when both trains will depart simultaneously, we need to find the LCM of 7 and 9. Since the LCM is 63, both trains will depart at the same time every 63 minutes.
2. Cutting Fabric:
You have two rolls of fabric, one 7 meters long and the other 9 meters long. You want to cut the fabric into pieces of equal length, using the entire length of both rolls without any waste. The LCM (63) gives the maximum length of the pieces you can cut, ensuring that all fabric is utilized efficiently.
3. Synchronizing Clocks:
Two digital clocks display the time differently. Clock A updates every 7 seconds, while Clock B updates every 9 seconds. To determine when both clocks will update simultaneously, calculate the LCM. They will synchronize every 63 seconds.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly efficient for this case. Simply find the prime factorization of each number and then take the highest power of each prime factor present in any of the factorizations. The product of these highest powers will be the LCM.
Conclusion
Finding the LCM of 7 and 9, while seemingly a simple problem, illustrates a fundamental concept in mathematics with far-reaching applications. Understanding different methods for calculating the LCM enhances problem-solving skills and provides valuable tools for tackling more complex mathematical challenges in various fields. The relationship between LCM and GCD further enriches our understanding of number theory and its practical relevance. Mastering the LCM concept empowers one to tackle real-world problems efficiently and effectively, ranging from scheduling to resource management. The methods outlined in this guide provide a solid foundation for exploring and applying this essential mathematical principle.
Latest Posts
Latest Posts
-
The Protein Coat Of A Virus Is Called
Mar 31, 2025
-
Melting Of Wax Is A Physical Or Chemical Change
Mar 31, 2025
-
What Is 35 Cm In Inches
Mar 31, 2025
-
How Many Feet In 44 Inches
Mar 31, 2025
-
What Is The Difference Between An Ecosystem And An Environment
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Least Common Factor Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
