Lcm Of 8 9 And 6
Juapaving
Mar 29, 2025 · 5 min read
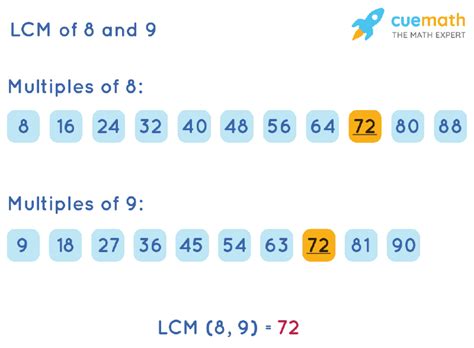
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 9, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling tasks to simplifying fractions. This article provides a thorough explanation of how to calculate the LCM of 8, 9, and 6, exploring different methods and delving into the underlying mathematical principles. We'll also examine real-world scenarios where understanding LCM proves beneficial.
Understanding Least Common Multiples (LCM)
Before diving into the calculation, let's define what a least common multiple is. The LCM of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that all the given numbers divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
This concept is crucial in various mathematical operations, including:
- Adding and subtracting fractions: Finding a common denominator is essential before adding or subtracting fractions, and the LCM of the denominators provides the least common denominator (LCD).
- Solving problems involving cyclical events: Imagine two events that occur at regular intervals. The LCM helps determine when both events will occur simultaneously.
- Simplifying expressions: LCM can simplify algebraic expressions and reduce them to their lowest terms.
Methods for Calculating the LCM of 8, 9, and 6
There are several approaches to calculating the LCM of 8, 9, and 6. Let's explore the most common methods:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...
By comparing the lists, we can see that the smallest number that appears in all three lists is 72. Therefore, the LCM of 8, 9, and 6 is 72.
This method becomes less efficient with larger numbers, as the lists can grow quite long before a common multiple is found.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a more systematic approach. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime factorization of 8: 2³
- Prime factorization of 9: 3²
- Prime factorization of 6: 2 x 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3² = 9
Now, multiply these highest powers together: 8 x 9 = 72. Therefore, the LCM of 8, 9, and 6 is 72.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. We can use the following formula to calculate the LCM:
LCM(a, b, c) = (|a x b x c|) / GCD(a, b, c)
First, we need to find the GCD of 8, 9, and 6. The GCD is the largest number that divides all three numbers without leaving a remainder. In this case, the GCD of 8, 9, and 6 is 1 (as they share no common factors other than 1).
Now, applying the formula:
LCM(8, 9, 6) = (8 x 9 x 6) / GCD(8, 9, 6) = 432 / 1 = 72
Choosing the Best Method
The best method for calculating the LCM depends on the numbers involved:
- Listing Multiples: Suitable for small numbers where the lists of multiples are manageable.
- Prime Factorization: The most efficient and systematic method for larger numbers.
- GCD Method: Useful when you already know or can easily calculate the GCD.
Real-World Applications of LCM
The concept of LCM has practical applications in various real-world scenarios:
-
Scheduling: Imagine you have three machines that need maintenance. Machine A needs maintenance every 8 days, Machine B every 9 days, and Machine C every 6 days. To find the next time all three machines will require maintenance simultaneously, you need to calculate the LCM of 8, 9, and 6, which is 72 days.
-
Fraction Operations: When adding or subtracting fractions, you need a common denominator. The LCM of the denominators provides the least common denominator (LCD), making the calculation simpler and more efficient. For example, adding 1/6 + 1/8 + 1/9 requires finding the LCM of 6, 8, and 9 (which is 72), resulting in 12/72 + 9/72 + 8/72 = 29/72.
-
Project Management: In project management, tasks often have dependencies and recurring cycles. LCM can help schedule tasks efficiently, ensuring that dependent tasks align appropriately.
-
Music Theory: LCM is used in music theory to determine the least common denominator for time signatures, ensuring rhythmic consistency.
Conclusion
Calculating the LCM is a fundamental mathematical skill with practical applications across diverse fields. While the listing multiples method offers a simple approach for smaller numbers, the prime factorization method provides a more efficient and systematic approach for larger numbers. Understanding the different methods and choosing the most appropriate one based on the context is crucial for effective problem-solving. By mastering the concept of LCM, you can efficiently tackle various mathematical problems and apply it to real-world scenarios, optimizing tasks and improving efficiency in many situations. Remember to practice using different methods to solidify your understanding and improve your speed and accuracy. The ability to find the LCM swiftly and accurately is a valuable asset in many academic and professional contexts.
Latest Posts
Latest Posts
-
70 As A Product Of Prime Factors
Mar 31, 2025
-
A Ray Has Two Endpoints True Or False
Mar 31, 2025
-
A Substance That Cannot Be Broken Down By Chemical Means
Mar 31, 2025
-
Do Both Prokaryotic And Eukaryotic Cells Have Ribosomes
Mar 31, 2025
-
Which Law Represents A Balanced Chemical Equation
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 9 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
