Lcm Of 5 10 And 3
Juapaving
Mar 24, 2025 · 5 min read
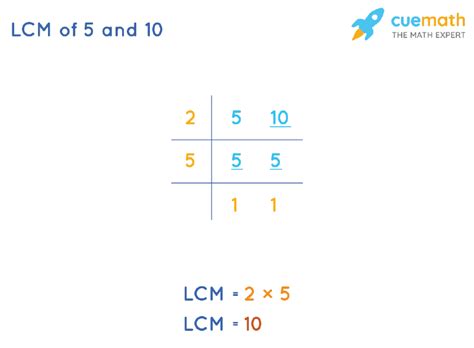
Table of Contents
Finding the Least Common Multiple (LCM) of 5, 10, and 3: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling tasks to simplifying fractions. This comprehensive guide will explore the LCM, focusing specifically on finding the LCM of 5, 10, and 3. We'll cover multiple methods, explain the underlying principles, and provide ample examples to solidify your understanding. By the end, you'll not only know the LCM of these specific numbers but also possess the skills to calculate the LCM of any set of numbers.
Understanding the Least Common Multiple (LCM)
Before diving into the calculation, let's establish a clear understanding of what the LCM represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that all the given numbers divide into evenly.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... The multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, making 6 the LCM of 2 and 3.
Method 1: Listing Multiples
This method is straightforward and intuitive, especially for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple.
Let's apply this method to find the LCM of 5, 10, and 3:
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, ...
By examining the lists, we can see that the smallest number common to all three lists is 30. Therefore, the LCM of 5, 10, and 3 is 30.
Method 2: Prime Factorization
This method is more efficient for larger numbers or when dealing with more than two numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
Let's break down the prime factorization for each number:
- 5: 5 (5 is a prime number)
- 10: 2 x 5
- 3: 3 (3 is a prime number)
Now, let's identify the highest power of each prime factor present in the factorizations:
- 2: The highest power of 2 is 2¹ (from 10).
- 3: The highest power of 3 is 3¹ (from 3).
- 5: The highest power of 5 is 5¹ (from both 5 and 10).
To find the LCM, we multiply these highest powers together:
LCM(5, 10, 3) = 2¹ x 3¹ x 5¹ = 2 x 3 x 5 = 30
This method confirms our result from the listing multiples method.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, although the calculation becomes more complex. For three numbers, a, b, and c, there isn't a direct equivalent, but we can use the pairwise LCM approach. We find the LCM of two numbers, then find the LCM of the result and the third number.
Let's apply this to our numbers:
- Find the GCD of 5 and 10. The GCD(5, 10) = 5.
- Calculate the LCM of 5 and 10 using the formula: LCM(5,10) * GCD(5,10) = 5*10; LCM(5,10) = 10.
- Now, find the LCM of the result (10) and 3. Using the prime factorization method:
- 10 = 2 x 5
- 3 = 3
- LCM(10, 3) = 2 x 3 x 5 = 30
Therefore, the LCM(5, 10, 3) = 30. Note that this method is more computationally intensive for larger sets of numbers, making prime factorization generally preferred for efficiency.
Applications of the LCM
The LCM has numerous practical applications across various fields:
1. Scheduling and Time Management:
Imagine you have two tasks: one that repeats every 5 days and another that repeats every 10 days. When will both tasks occur on the same day again? The LCM(5, 10) = 10, meaning both tasks will coincide every 10 days. This principle extends to more complex scheduling problems involving multiple repeating events.
2. Fraction Arithmetic:
Adding and subtracting fractions require a common denominator, which is the LCM of the denominators. For example, to add 1/5 and 1/3, we find the LCM of 5 and 3 (which is 15), and then rewrite the fractions with a denominator of 15 before adding them.
3. Gear Ratios and Mechanical Engineering:
In mechanical systems with multiple gears, the LCM helps determine the synchronization of gear rotations.
4. Music Theory:
Finding the LCM is crucial in music theory when dealing with rhythmic patterns and determining when different rhythms coincide.
5. Computer Science:
In computer programming, the LCM can be used in various algorithms and data structures, such as finding the least common multiple of array elements or solving problems related to cyclical events.
Conclusion
Finding the least common multiple is a fundamental mathematical operation with significant practical applications. While the listing multiples method is intuitive for smaller numbers, prime factorization provides a more efficient and systematic approach for larger numbers and more complex scenarios. Understanding these methods empowers you to solve a wide range of problems involving multiples and common factors, from simple fraction arithmetic to complex scheduling challenges. The LCM of 5, 10, and 3, as we've demonstrated through various methods, is definitively 30. Now you're equipped to tackle any LCM problem with confidence!
Latest Posts
Latest Posts
-
Write 70 As A Product Of Prime Factors
Mar 28, 2025
-
What Is The Lcm Of 2 And 8
Mar 28, 2025
-
What Is The Name Of Mg No3 2
Mar 28, 2025
-
Which Of The Following Is True About Hiv
Mar 28, 2025
-
In Which Situation Is The Distance Traveled Proportional To Time
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 10 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
