Lcm Of 4 3 And 6
Juapaving
Mar 24, 2025 · 5 min read
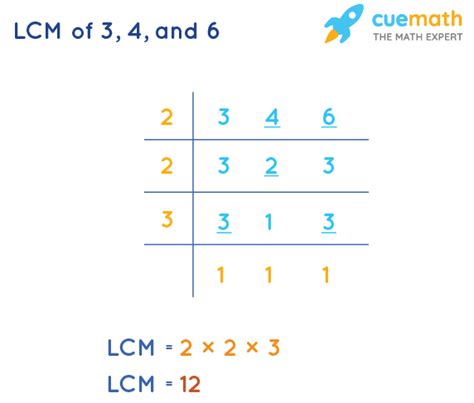
Table of Contents
Finding the LCM of 4, 3, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling and project management to music theory and cryptography. This article provides a comprehensive exploration of how to find the LCM of 4, 3, and 6, illustrating different methods and highlighting the underlying mathematical principles. We'll delve deeper than a simple solution, exploring the concept's significance and offering practical applications to solidify your understanding.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 4, 3, and 6, let's establish a clear understanding of what the LCM represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
Why is LCM important?
The LCM has practical applications in various scenarios:
- Scheduling: Determining when events will occur simultaneously. For instance, if three buses depart from a station at intervals of 4, 3, and 6 hours respectively, the LCM will tell you when they'll all depart at the same time.
- Fraction Operations: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is essentially the LCM of the denominators.
- Music Theory: Determining the least common multiple of note durations to find rhythmic patterns.
- Project Management: Synchronizing tasks with different completion times.
- Cryptography: Certain encryption algorithms use LCM calculations.
Methods for Finding the LCM of 4, 3, and 6
Several methods exist for determining the LCM of a set of numbers. Let's explore the most common approaches, applying them to our example of 4, 3, and 6.
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
By comparing the lists, we can see that the smallest number appearing in all three lists is 12. Therefore, the LCM of 4, 3, and 6 is 12.
2. Prime Factorization Method
This method is more efficient for larger numbers and offers a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime factorization of 4: 2²
- Prime factorization of 3: 3¹
- Prime factorization of 6: 2¹ * 3¹
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2² = 4
- Highest power of 3: 3¹ = 3
Now, multiply these highest powers together: 4 * 3 = 12. The LCM of 4, 3, and 6 is 12.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of a set of numbers are related. We can use the relationship:
LCM(a, b, c) = (|a * b * c|) / GCD(a, b, c)
However, this method is more complex when dealing with multiple numbers, requiring multiple GCD calculations. Let's illustrate using the concept of pairwise GCD.
First, we find the GCD of two numbers, then use that result to find the GCD with the remaining number.
- GCD(4,3) = 1 (4 = 2², 3 = 3; No common factors)
- GCD(1,6) = 1
Applying the formula, we get: LCM = (4 * 3 * 6) / 1 = 72. This approach is flawed for multiple numbers; it’s not as straightforward as the other methods to compute LCM for 4, 3, and 6. The prime factorization method is generally preferred for accuracy and efficiency in such cases.
4. Ladder Method or Staircase Method
This visual method organizes the process clearly, particularly beneficial for larger sets of numbers.
2 | 4 3 6
2 | 2 3 3
3 | 1 3 3
| 1 1 1
We successively divide the numbers by their common prime factors. The LCM is the product of all the divisors used: 2 * 2 * 3 = 12.
Advanced Concepts and Applications
The LCM concept extends beyond simple calculations. Understanding the underlying principles allows for more complex problem-solving:
-
Finding the LCM of more than three numbers: The prime factorization method and the ladder method scale efficiently to handle larger sets of numbers. Simply extend the process to include all numbers in the set.
-
LCM and the least common denominator (LCD): When adding or subtracting fractions with different denominators, finding the LCD (which is the LCM of the denominators) is crucial to obtain a common denominator for simplifying the calculation.
-
LCM in modular arithmetic: LCM plays a crucial role in solving congruences and problems in modular arithmetic, a branch of number theory with significant applications in cryptography and computer science.
-
LCM in scheduling and project management: The LCM helps to determine the optimal time for events to occur simultaneously or to coordinate tasks with different durations. For example, imagine three machines in a factory completing cycles in 4, 3, and 6 hours, respectively. The LCM (12 hours) indicates when all machines will simultaneously complete a cycle, which could be vital for efficient production scheduling.
Conclusion
Calculating the least common multiple (LCM) is a fundamental skill with far-reaching implications. This article has explored different methods for calculating the LCM of 4, 3, and 6, demonstrating that the answer is 12. We've moved beyond a simple solution to explore the underlying mathematics, emphasizing the importance of the LCM in various applications. Choosing the most suitable method depends on the numbers involved and the context of the problem. The prime factorization method is often preferred for its efficiency and clarity, particularly when dealing with larger numbers or more complex scenarios. Understanding LCM strengthens mathematical foundations and opens doors to solving more intricate problems in various fields.
Latest Posts
Latest Posts
-
Least Common Multiple Of 6 8 And 15
Mar 29, 2025
-
What Is The Lcm Of 5 And 7
Mar 29, 2025
-
Least Common Multiple Of 6 9 And 15
Mar 29, 2025
-
Words Beginning And Ending In T
Mar 29, 2025
-
Light Microscope Vs Transmission Electron Microscope
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 3 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
