Find The Complementary And Supplementary Angles
Juapaving
Apr 01, 2025 · 5 min read
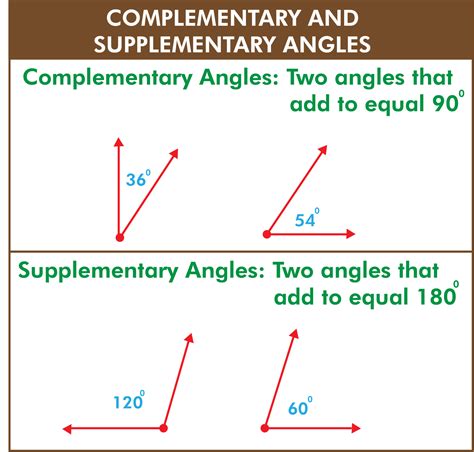
Table of Contents
Finding Complementary and Supplementary Angles: A Comprehensive Guide
Understanding complementary and supplementary angles is fundamental to geometry and trigonometry. This comprehensive guide will delve into the definitions, properties, and applications of these crucial angle relationships, providing you with a solid foundation and practical examples to master the concept.
What are Complementary Angles?
Complementary angles are two angles whose measures add up to 90 degrees (a right angle). Think of it like completing a puzzle: two complementary angles perfectly "complement" each other to form a right angle. Crucially, complementary angles don't have to be adjacent (next to each other). They simply need to add up to 90°.
Example:
- Angle A = 30°
- Angle B = 60°
Angle A and Angle B are complementary because 30° + 60° = 90°.
Finding Complementary Angles: Methods and Examples
Let's explore different scenarios and methods to find complementary angles:
1. One Angle is Known:
If you know the measure of one angle, finding its complement is straightforward: subtract the known angle from 90°.
Example: If Angle X = 25°, its complement is 90° - 25° = 65°.
2. Algebraic Approach:
Problems often involve variables. Let's say we have two complementary angles, x and y. We can represent their relationship using the equation:
x + y = 90°
If we know the value of x, we can solve for y, and vice versa.
Example: If x = 2x + 10°, then:
2x + 10° + y = 90° y = 90° - 2x - 10° y = 80° - 2x
To find the value of y, we'd need additional information, such as the value of x or another equation relating x and y.
3. Real-World Applications:
Complementary angles pop up in everyday situations, often unnoticed. Consider:
- Architecture: The corners of a rectangular room form four right angles, each composed of two complementary angles.
- Construction: Carpenters and builders frequently use complementary angles when working with right angles.
- Graphic Design: Creating visually appealing designs often involves using complementary angles to achieve balance and harmony.
What are Supplementary Angles?
Supplementary angles are two angles whose measures add up to 180 degrees (a straight angle). Unlike complementary angles, which form a right angle, supplementary angles form a straight line. Again, they don't have to be adjacent.
Example:
- Angle C = 110°
- Angle D = 70°
Angle C and Angle D are supplementary because 110° + 70° = 180°.
Finding Supplementary Angles: Methods and Examples
Similar to complementary angles, let's explore different methods for finding supplementary angles:
1. One Angle is Known:
If you know one angle's measure, subtract it from 180° to find its supplement.
Example: If Angle Z = 135°, its supplement is 180° - 135° = 45°.
2. Algebraic Approach:
Again, we can use algebraic equations to represent the relationship between supplementary angles. Let's say we have two supplementary angles, a and b. The equation would be:
a + b = 180°
We can solve for one variable if we know the value of the other.
Example: If a = 3a - 20°, then:
3a - 20° + b = 180° b = 180° - 3a + 20° b = 200° - 3a
This equation allows us to calculate 'b' once we know 'a'.
3. Real-World Applications:
Supplementary angles are extensively used in various fields:
- Navigation: Determining directions and bearings often involves using supplementary angles.
- Engineering: Supplementary angles are crucial for designing stable structures and calculating forces.
- Computer Graphics: Creating realistic 3D models often requires precise calculations involving supplementary angles.
Complementary vs. Supplementary Angles: A Comparison
| Feature | Complementary Angles | Supplementary Angles |
|---|---|---|
| Sum | 90° | 180° |
| Formation | Forms a right angle | Forms a straight angle |
| Adjacency | Not necessarily adjacent | Not necessarily adjacent |
| Finding Complement/Supplement | Subtract from 90° / 180° | Subtract from 180° / 90° |
Solving Problems Involving Complementary and Supplementary Angles
Let's delve into some practical problems to solidify your understanding:
Problem 1: Two angles are complementary. One angle is twice the measure of the other. Find the measure of each angle.
Solution:
Let the smaller angle be x. The larger angle is 2x. Since they are complementary:
x + 2x = 90° 3x = 90° x = 30°
Therefore, the smaller angle is 30°, and the larger angle is 2 * 30° = 60°.
Problem 2: Two angles are supplementary. One angle is 30° more than the other. Find the measure of each angle.
Solution:
Let one angle be x. The other angle is x + 30°. Since they are supplementary:
x + (x + 30°) = 180° 2x + 30° = 180° 2x = 150° x = 75°
Therefore, one angle is 75°, and the other is 75° + 30° = 105°.
Problem 3: Angle A and Angle B are complementary. Angle A is 15° less than Angle B. Find the measures of Angle A and Angle B.
Solution:
Let Angle B = x. Then Angle A = x - 15°. Since they are complementary:
x + (x - 15°) = 90° 2x - 15° = 90° 2x = 105° x = 52.5°
Therefore, Angle B = 52.5°, and Angle A = 52.5° - 15° = 37.5°.
Advanced Concepts and Applications
The concepts of complementary and supplementary angles extend into more complex geometric problems and trigonometric calculations. Here are a few examples:
- Triangle Angle Sum Theorem: The angles in any triangle always add up to 180°. This theorem often involves working with supplementary angles.
- Polygon Angle Sums: The sum of interior angles in a polygon is dependent on the number of sides and often relies on understanding supplementary and complementary angles for calculations.
- Trigonometry: Many trigonometric identities and formulas rely on the relationships between complementary and supplementary angles.
Understanding complementary and supplementary angles is a cornerstone of geometry and beyond. By mastering these fundamental concepts and practicing problem-solving techniques, you'll be well-equipped to tackle more complex geometric and trigonometric challenges. Remember to practice regularly, and you'll soon find yourself confidently solving problems involving these essential angle relationships.
Latest Posts
Latest Posts
-
Magnetic Field From A Current Loop
Apr 02, 2025
-
Collection Of Nerve Cell Bodies Outside The Cns
Apr 02, 2025
-
What Do Nitrification And Denitrification Have In Common
Apr 02, 2025
-
What Is The Lowest Common Multiple Of 3 And 7
Apr 02, 2025
-
How To Find A Supplementary Angle
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Find The Complementary And Supplementary Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
