Is Pressure Directly Proportional To Temperature
Juapaving
Apr 01, 2025 · 5 min read
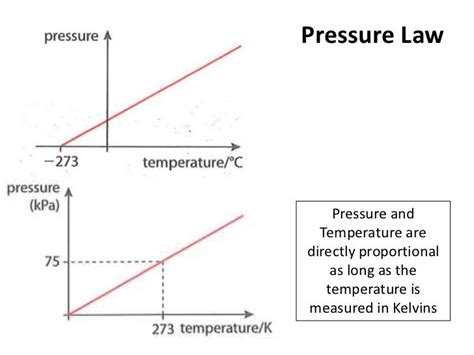
Table of Contents
Is Pressure Directly Proportional to Temperature? Exploring the Relationship Between Pressure and Temperature in Gases
The relationship between pressure and temperature in gases is a fundamental concept in physics and chemistry, with far-reaching implications in various fields, from meteorology to engineering. A common question that arises is: Is pressure directly proportional to temperature? The short answer is: it depends. While a direct proportionality exists under specific conditions, a more nuanced understanding requires exploring the ideal gas law and its limitations.
Understanding the Ideal Gas Law
The foundation for understanding the pressure-temperature relationship lies in the ideal gas law: PV = nRT. Let's break down each component:
- P: Pressure (typically measured in Pascals, atmospheres, or mmHg)
- V: Volume (typically measured in liters or cubic meters)
- n: Number of moles of gas (a measure of the amount of gas)
- R: The ideal gas constant (a proportionality constant that depends on the units used for other variables)
- T: Temperature (must be expressed in Kelvin – the absolute temperature scale)
If we hold the number of moles (n) and volume (V) constant, the ideal gas law simplifies to: P/T = constant or P ∝ T. This signifies a direct proportionality between pressure and temperature under constant volume and number of moles. This relationship is often referred to as Gay-Lussac's Law.
Gay-Lussac's Law: The Direct Proportionality Under Constant Volume
Gay-Lussac's Law states that at constant volume, the pressure of a given mass of gas is directly proportional to its absolute temperature. This means if you double the absolute temperature, you double the pressure, provided the volume remains unchanged. This is a crucial finding that directly answers the question posed in the title, but only under specific conditions.
Illustrative Example: Consider a sealed container of gas at room temperature and pressure. If you increase the temperature (in Kelvin), the gas molecules move faster, colliding more frequently and forcefully with the container walls, resulting in a higher pressure. Conversely, decreasing the temperature reduces the kinetic energy of the gas molecules, leading to lower pressure.
The Importance of the Absolute Temperature Scale (Kelvin)
It's crucial to emphasize the use of the Kelvin scale for temperature in the ideal gas law and Gay-Lussac's Law. The Kelvin scale is an absolute temperature scale, meaning its zero point represents the absence of all thermal energy. Using Celsius or Fahrenheit would introduce inaccuracies because these scales have arbitrary zero points. The Kelvin scale ensures that the proportionality holds true: zero pressure only occurs at absolute zero (0 Kelvin).
Limitations of the Ideal Gas Law and Departures from Direct Proportionality
The ideal gas law is a simplification; real gases don't always behave ideally. Several factors can cause deviations from the direct proportionality between pressure and temperature:
1. Intermolecular Forces:
Real gas molecules possess intermolecular forces (attractive or repulsive forces between molecules). These forces become significant at higher pressures and lower temperatures. Attractive forces reduce the effective pressure, while repulsive forces increase it. These forces disrupt the simple direct proportionality predicted by the ideal gas law.
2. Molecular Volume:
The ideal gas law assumes that gas molecules are point masses with negligible volume. In reality, gas molecules occupy a finite volume, which becomes more significant at high pressures. This molecular volume reduces the available space for the molecules to move, affecting the pressure-temperature relationship.
3. Non-Ideal Behavior at High Pressures and Low Temperatures:
At high pressures and low temperatures, the deviations from ideal gas behavior become significant. Under these conditions, the intermolecular forces and molecular volume can no longer be neglected, leading to a non-linear relationship between pressure and temperature.
4. Chemical Reactions:
If the gas undergoes a chemical reaction with a change in the number of moles, the pressure-temperature relationship will be affected. Gay-Lussac's Law specifically requires a constant amount of gas (constant 'n'). Any reaction altering the number of moles violates this condition.
Beyond Gay-Lussac's Law: Real Gas Equations of State
To account for the non-ideal behavior of real gases, more complex equations of state are used. These equations, such as the van der Waals equation, incorporate correction terms to account for intermolecular forces and molecular volume. These equations provide a more accurate description of the pressure-temperature relationship for real gases under various conditions.
Applications and Real-World Examples
The pressure-temperature relationship has numerous applications across diverse fields:
-
Internal Combustion Engines: The pressure-temperature relationship is crucial in understanding the operation of internal combustion engines. The combustion process raises the temperature and pressure of the gases, driving the piston.
-
Weather Forecasting: Atmospheric pressure and temperature variations are essential factors in weather forecasting models. Changes in temperature affect air pressure, influencing weather patterns.
-
Aerospace Engineering: The pressure-temperature relationship is crucial in designing aircraft and spacecraft, considering the changes in atmospheric pressure and temperature at different altitudes.
-
Refrigeration and Air Conditioning: Refrigeration systems utilize the pressure-temperature relationship to transfer heat. Refrigerants change phase, absorbing heat during evaporation (lower pressure) and releasing heat during condensation (higher pressure).
Conclusion: Nuances in the Pressure-Temperature Relationship
While Gay-Lussac's Law establishes a direct proportionality between pressure and temperature for an ideal gas at constant volume, it's crucial to understand its limitations. Real gases exhibit deviations from ideal behavior, especially at high pressures and low temperatures. Intermolecular forces and molecular volume significantly influence the pressure-temperature relationship under these conditions. For accurate predictions, more sophisticated equations of state, which consider these deviations, are necessary. The principle remains a cornerstone of thermodynamics, with wide applications in various scientific and engineering disciplines, requiring careful consideration of the specific conditions involved to accurately predict the relationship between pressure and temperature. Remember to always work in Kelvin when using equations based on the ideal gas law to ensure accurate calculations. Understanding the intricacies of this relationship is critical for accurate modeling and prediction in numerous fields.
Latest Posts
Latest Posts
-
Is 17 A Prime Number Or A Composite Number
Apr 02, 2025
-
Is Burning A Candle A Chemical Or Physical Change
Apr 02, 2025
-
What Is The State Of Matter Of Fire
Apr 02, 2025
-
Give Two Similarities And Two Differences Between Gymnosperms And Angiosperms
Apr 02, 2025
-
Largest Cell Of The Human Body
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Is Pressure Directly Proportional To Temperature . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
