Is 3 5 Bigger Than 3 4
Juapaving
May 10, 2025 · 4 min read
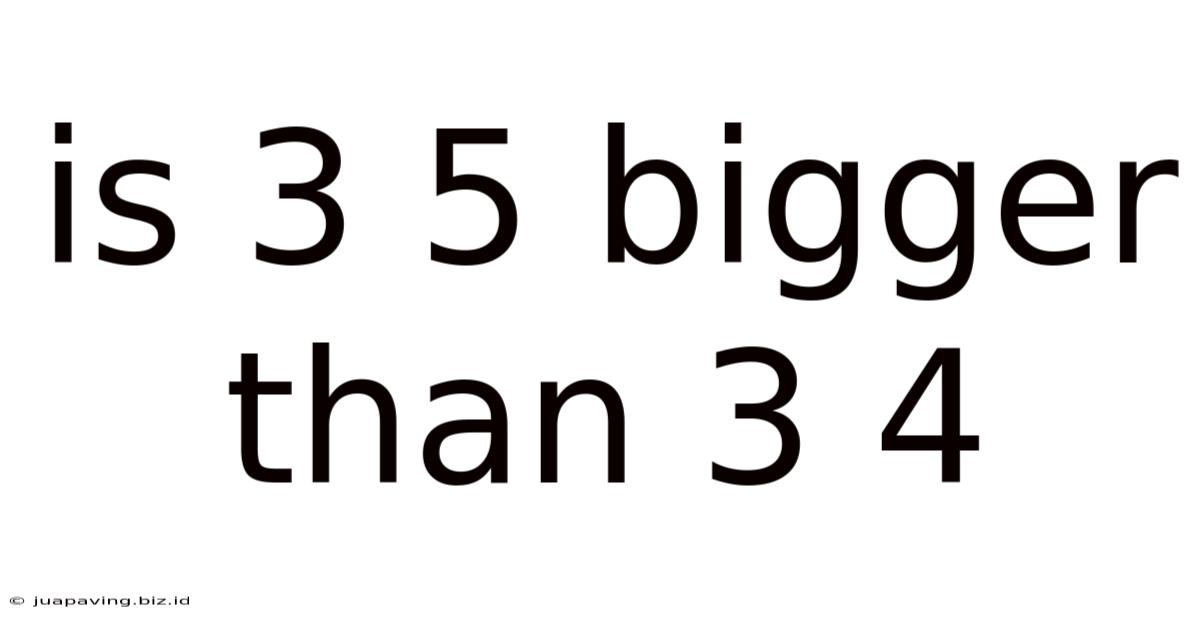
Table of Contents
Is 3.5 Bigger Than 3.4? A Deep Dive into Decimal Comparison
The question, "Is 3.5 bigger than 3.4?" might seem trivial at first glance. For many, the answer is immediately apparent. However, a deeper exploration of this seemingly simple comparison provides an excellent opportunity to delve into the fundamental concepts of decimal numbers, number systems, and the principles of comparison. This article will not only answer the question directly but also explore the underlying mathematical principles, providing a comprehensive understanding of decimal number comparison and its practical applications.
Understanding Decimal Numbers
Before we directly compare 3.5 and 3.4, let's refresh our understanding of decimal numbers. Decimal numbers, also known as base-10 numbers, are the most commonly used number system in the world. They use ten digits (0-9) to represent numbers, and the position of each digit determines its value. The decimal point separates the whole number part from the fractional part.
Components of a Decimal Number:
- Whole Number Part: The digits to the left of the decimal point represent the whole number. In our example, both 3.5 and 3.4 have a whole number part of 3.
- Fractional Part: The digits to the right of the decimal point represent the fractional part, or the part less than one. In 3.5, the fractional part is 0.5 (five-tenths), and in 3.4, the fractional part is 0.4 (four-tenths).
Place Value: Each position to the right of the decimal point represents a decreasing power of 10. The first position is tenths (1/10), the second is hundredths (1/100), the third is thousandths (1/1000), and so on.
Direct Comparison: 3.5 vs 3.4
Now, let's directly compare 3.5 and 3.4. Since both numbers have the same whole number part (3), we need to compare their fractional parts: 0.5 and 0.4.
Visual Representation: Imagine a number line. 3.5 would be located further to the right than 3.4. This visual representation immediately demonstrates that 3.5 is greater than 3.4.
Numerical Comparison: We can also compare the numbers directly by comparing their tenths place. 0.5 (five-tenths) is greater than 0.4 (four-tenths). Therefore, 3.5 is bigger than 3.4.
Therefore, the answer is a resounding YES. 3.5 is bigger than 3.4.
Expanding the Understanding: Different Decimal Comparisons
While comparing 3.5 and 3.4 is straightforward, let's expand our understanding by exploring more complex decimal comparisons.
Comparing Decimals with Different Numbers of Decimal Places
Consider comparing 3.5 and 3.45. At first glance, it might seem that 3.45 is larger because it has more digits after the decimal point. However, this is incorrect.
To compare, we can add a zero to 3.5, making it 3.50. Now we can easily compare 3.50 and 3.45. Since 50 hundredths is greater than 45 hundredths, 3.50 (or 3.5) is still larger than 3.45.
Comparing Decimals with More Than One Decimal Place
Let's compare 2.785 and 2.79. Again, we can add a zero to 2.79 to make it 2.790. Now, comparing 2.785 and 2.790, we see that 2.790 (or 2.79) is larger because 790 thousandths is greater than 785 thousandths.
Negative Decimal Numbers
The principles of comparison remain the same when dealing with negative decimal numbers. However, remember that the further a number is to the left on the number line (more negative), the smaller it is. Therefore, -3.5 is smaller than -3.4.
Practical Applications of Decimal Comparison
The ability to compare decimal numbers is crucial in various aspects of life:
- Finance: Comparing prices, calculating discounts, managing bank accounts, and analyzing financial statements all require accurate decimal comparisons.
- Science: In scientific measurements, precision is critical, and comparing decimal values is essential for analysis and experimentation.
- Engineering: In engineering designs and calculations, decimal numbers are used extensively, and accurate comparisons are needed for precision and safety.
- Everyday Life: From measuring ingredients in cooking to calculating distances, decimal comparisons are part of our daily routines.
Beyond Simple Comparisons: Understanding Ordering and Magnitude
Comparing decimals isn't just about determining whether one is bigger or smaller; it's about understanding their relative positions and magnitudes within the number system. This understanding is vital for more advanced mathematical operations.
Ordering Decimals: The ability to compare decimals allows us to order a series of decimals from least to greatest or greatest to least. This skill is fundamental in data analysis and sorting.
Magnitude of Decimals: Understanding the magnitude of decimals helps us understand their relative sizes and importance within a context. For instance, in scientific measurements, a small difference in decimal values might be significant, while in other scenarios, it may be negligible.
Conclusion: Mastering Decimal Comparisons
The simple question, "Is 3.5 bigger than 3.4?" opens a door to a deeper exploration of decimal numbers and their comparison. This article has not only provided the answer but also expanded upon the underlying principles, providing a comprehensive understanding of decimal comparison techniques. Mastering this fundamental skill is essential for success in various fields, from everyday tasks to complex scientific and financial calculations. The ability to accurately compare decimals is a cornerstone of numerical literacy and a valuable skill for anyone seeking to navigate the quantitative aspects of the world. Remember, the seemingly simple can often lead to profound understanding when explored thoroughly.
Latest Posts
Latest Posts
-
What Fractions Are Equivalent To 1 4
May 10, 2025
-
Words With Ou Sound Like U
May 10, 2025
-
What Organism Can Make Its Own Food
May 10, 2025
-
What Part Does Chlorophyll Play In Photosynthesis
May 10, 2025
-
What Is The Colour Of Sulphuric Acid
May 10, 2025
Related Post
Thank you for visiting our website which covers about Is 3 5 Bigger Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.