What Fractions Are Equivalent To 1/4
Juapaving
May 10, 2025 · 5 min read
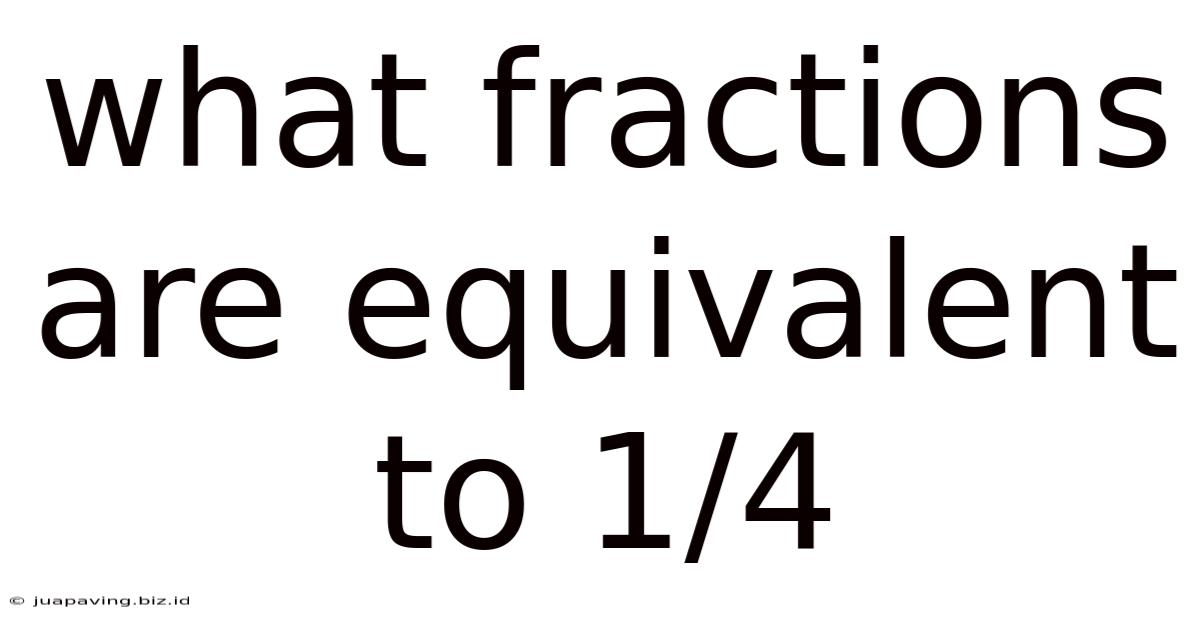
Table of Contents
What Fractions are Equivalent to 1/4? A Comprehensive Guide
Understanding equivalent fractions is a cornerstone of mathematics, crucial for everything from basic arithmetic to advanced calculus. This comprehensive guide dives deep into the concept of equivalent fractions, specifically focusing on fractions equivalent to 1/4. We'll explore the underlying principles, demonstrate various methods for finding these equivalents, and offer practical applications to solidify your understanding.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they look different. Imagine slicing a pizza: If you cut it into four equal slices and take one, you have 1/4 of the pizza. Now, imagine cutting the same pizza into eight equal slices. Taking two of those smaller slices still gives you the same amount of pizza – half of the original quarter. This illustrates the concept of equivalence: 1/4 and 2/8 represent the same quantity.
The key to finding equivalent fractions lies in multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number. This process maintains the ratio, ensuring the fractions remain equivalent.
Methods for Finding Equivalent Fractions of 1/4
Several methods can effectively identify fractions equivalent to 1/4. Let's explore some of the most common and efficient approaches:
1. Multiplying the Numerator and Denominator
The simplest method involves multiplying both the numerator and denominator of 1/4 by the same whole number. Let's see some examples:
- Multiplying by 2: (1 x 2) / (4 x 2) = 2/8
- Multiplying by 3: (1 x 3) / (4 x 3) = 3/12
- Multiplying by 4: (1 x 4) / (4 x 4) = 4/16
- Multiplying by 5: (1 x 5) / (4 x 5) = 5/20
- Multiplying by 10: (1 x 10) / (4 x 10) = 10/40
And so on. You can continue this process indefinitely, generating an infinite number of fractions equivalent to 1/4. Each resulting fraction represents the same portion or value.
2. Using a Common Factor
This method involves finding a common factor (a number that divides both the numerator and denominator without leaving a remainder) and simplifying the fraction. While this doesn't directly generate equivalent fractions, it helps identify if a given fraction is equivalent to 1/4. For instance, consider the fraction 12/48. Both 12 and 48 are divisible by 12:
12 ÷ 12 = 1 48 ÷ 12 = 4
Therefore, 12/48 simplifies to 1/4, proving its equivalence.
3. Visual Representation
A visual approach can be particularly helpful for beginners. Imagine a square representing a whole unit. Divide this square into four equal parts. Shading one part visually represents 1/4. Now, divide the same square into eight equal parts. Shading two of these smaller parts clearly shows the equivalence to the original shaded area (1/4). This method extends to other divisions (12 parts, 16 parts, and so on).
Applications of Equivalent Fractions
The concept of equivalent fractions is fundamental to many mathematical operations and real-world applications:
1. Simplifying Fractions
Simplifying fractions, also known as reducing fractions to their lowest terms, involves finding the greatest common factor (GCF) of the numerator and denominator and dividing both by it. This results in an equivalent fraction but in its simplest form. For example, 20/80 simplifies to 1/4.
2. Adding and Subtracting Fractions
Before adding or subtracting fractions, they must have a common denominator. Finding equivalent fractions with the least common multiple (LCM) as the denominator is crucial for performing these operations accurately.
3. Comparing Fractions
Determining which of two fractions is larger or smaller often requires finding equivalent fractions with a common denominator. This allows for direct comparison of the numerators.
4. Ratios and Proportions
Ratios and proportions are extensively used in various fields, including cooking, engineering, and finance. Understanding equivalent fractions is essential for solving problems involving ratios and proportions.
5. Percentages and Decimals
Converting fractions to percentages and decimals often involves finding equivalent fractions. For example, 1/4 is equivalent to 25% and 0.25.
Infinite Equivalents: The Unending Possibilities
It's important to note that there are infinitely many fractions equivalent to 1/4. Any fraction obtained by multiplying both the numerator and the denominator of 1/4 by the same whole number will be equivalent. This illustrates the rich and expansive nature of the concept of equivalent fractions.
Beyond the Basics: Exploring More Complex Scenarios
While the core concept of equivalent fractions is relatively straightforward, it underpins more complex mathematical operations. Let's explore some scenarios:
-
Fractions with larger numbers: Finding equivalent fractions for larger numbers requires careful attention to common factors and simplifying. For example, determining if 75/300 is equivalent to 1/4 involves simplifying 75/300 by finding the greatest common divisor (GCD) of 75 and 300, which is 75. Dividing both numerator and denominator by 75 yields 1/4, confirming the equivalence.
-
Algebraic fractions: Equivalent fractions extend to algebraic expressions. For instance, consider the algebraic fraction (x/4x). Since 'x' is a common factor to both the numerator and the denominator, simplifying this fraction gives us 1/4.
-
Real-world problems involving fractions: Many practical situations involve equivalent fractions. If a recipe calls for 1/4 cup of sugar, understanding equivalent fractions allows for adjustments based on the available measuring tools. If you only have a 1/8 cup measuring cup, you'll know you need 2/8 (which is equivalent to 1/4) cup of sugar.
-
Working with mixed numbers: When working with mixed numbers (a whole number and a fraction), converting them to improper fractions (numerator larger than the denominator) is often necessary before finding equivalent fractions.
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is an essential skill in mathematics, offering practical applications in diverse fields. The seemingly simple concept of multiplying or dividing both the numerator and denominator by the same number hides a wealth of mathematical principles and problem-solving potential. By mastering this concept, you lay a strong foundation for more advanced mathematical studies and enhance your ability to solve real-world problems that involve proportions, ratios, and measurements. Remember, the journey into the world of fractions is ongoing; the more you explore, the deeper your understanding will become. So continue to practice, explore, and apply this knowledge – and watch your mathematical skills flourish!
Latest Posts
Latest Posts
-
What Are Five Life Functions Of Cells
May 10, 2025
-
Why Cooking An Egg Is A Chemical Change
May 10, 2025
-
Common Factors Of 12 And 28
May 10, 2025
-
How Many Perpendicular Lines Does A Square Have
May 10, 2025
-
Describe The Role Of Chlorophyll In Photosynthesis
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Fractions Are Equivalent To 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.