How To Find Period Of A Trig Eqn
Juapaving
Apr 02, 2025 · 5 min read
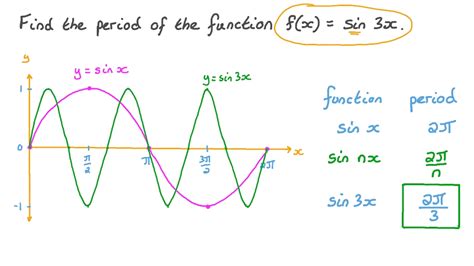
Table of Contents
How to Find the Period of a Trigonometric Equation
Determining the period of a trigonometric equation is a fundamental concept in trigonometry and crucial for understanding the cyclical nature of trigonometric functions. This comprehensive guide will walk you through various methods and techniques to find the period of different trigonometric equations, from simple sine and cosine functions to more complex combinations. We'll explore both the theoretical underpinnings and practical applications, providing you with a solid understanding of this important topic.
Understanding the Basic Periods
Before diving into complex equations, let's solidify our understanding of the basic periods of the primary trigonometric functions:
-
Sine (sin x): The period of the sine function is 2π. This means that the graph of y = sin x repeats its pattern every 2π units along the x-axis.
-
Cosine (cos x): Similar to the sine function, the cosine function also has a period of 2π. The graph of y = cos x repeats its pattern every 2π units.
-
Tangent (tan x): The tangent function has a period of π. This means its graph repeats every π units. It's important to note that the tangent function has vertical asymptotes, unlike sine and cosine.
-
Cosecant (csc x): The cosecant function, being the reciprocal of the sine function, also has a period of 2π.
-
Secant (sec x): As the reciprocal of the cosine function, the secant function also has a period of 2π.
-
Cotangent (cot x): The cotangent function, the reciprocal of the tangent function, has a period of π.
Finding the Period of Transformations of Basic Trig Functions
Understanding the impact of transformations on the period of trigonometric functions is critical. Let's consider a general form:
y = A sin(Bx + C) + D (or cosine, tangent, etc.)
Where:
- A: Amplitude (affects the vertical stretch/compression, but not the period).
- B: Affects the horizontal stretch/compression, and therefore directly influences the period.
- C: Phase shift (horizontal translation, doesn't affect the period).
- D: Vertical shift (vertical translation, doesn't affect the period).
The key to finding the period of a transformed trigonometric function lies in the value of 'B'.
The formula to calculate the period (P) is:
P = (Period of basic function) / |B|
Let's illustrate with examples:
Example 1: Find the period of y = 2sin(3x + π/2) + 1
Here, the basic function is sin x, with a period of 2π. B = 3. Therefore, the period is:
P = 2π / |3| = (2π)/3
Example 2: Find the period of y = -cos(x/2)
The basic function is cos x, with a period of 2π. B = 1/2. Therefore, the period is:
P = 2π / |1/2| = 4π
Example 3: Find the period of y = tan(4x - π)
The basic function is tan x, with a period of π. B = 4. Therefore, the period is:
P = π / |4| = π/4
Dealing with Combined Trigonometric Functions
Finding the period of equations involving multiple trigonometric functions requires a bit more care. The period of the combined function is usually the least common multiple (LCM) of the individual periods.
Example 4: Find the period of y = sin(2x) + cos(x)
- The period of sin(2x) is 2π / |2| = π
- The period of cos(x) is 2π
The LCM of π and 2π is 2π. Therefore, the period of the combined function is 2π.
Example 5: Find the period of y = tan(x/3) + cot(2x)
- The period of tan(x/3) is π / |1/3| = 3π
- The period of cot(2x) is π / |2| = π/2
To find the LCM of 3π and π/2, it's helpful to express them with a common denominator:
3π = 6π/2 π/2 = π/2
The LCM of 6π/2 and π/2 is 6π/2 = 3π. Therefore, the period of the combined function is 3π.
Handling More Complex Scenarios
Some equations might involve trigonometric functions within other trigonometric functions or complex combinations of functions and transformations. These cases require a systematic approach:
Example 6: Find the period of y = sin(sin(x))
This is a composition of trigonometric functions. The inner function sin(x) has a period of 2π. However, the outer function sin( ) doesn't change the fundamental period. Intuitively, since the sine function itself has a range between -1 and 1, the period doesn't change significantly. Analyzing the graph numerically would confirm that the period remains 2π.
Example 7: Finding the period of y = sin(x) + cos(2x) + tan(x/3)
-
Identify individual periods:
- sin(x): Period = 2π
- cos(2x): Period = 2π/2 = π
- tan(x/3): Period = π/(1/3) = 3π
-
Find the least common multiple (LCM): Find the LCM of 2π, π, and 3π. The easiest way is to consider the multiples:
- Multiples of 2π: 2π, 4π, 6π...
- Multiples of π: π, 2π, 3π, 4π, 5π, 6π...
- Multiples of 3π: 3π, 6π...
The LCM is 6π. This is the period of the combined function.
Graphical Verification
While the formulas provide accurate calculations, visualizing the graph of the function can offer valuable confirmation. Graphing calculators or software like Desmos or GeoGebra allow you to plot the function and visually inspect the repeating pattern to verify the calculated period.
Common Mistakes to Avoid
-
Ignoring the absolute value of B: Remember that the period formula uses the absolute value of B to ensure the period is always positive.
-
Incorrectly finding the LCM: Ensure you correctly determine the least common multiple of the individual periods when dealing with combined functions. Consider converting periods to a common denominator to simplify the LCM calculation.
-
Overlooking nested functions: Be mindful of nested trigonometric functions; the inner function's behavior will directly influence the outer function's period.
-
Not accounting for phase shifts: While phase shifts affect the horizontal positioning of the graph, they don't alter the period itself. Focus solely on the coefficient of 'x' inside the trigonometric function.
Conclusion
Finding the period of a trigonometric equation is a crucial skill in understanding and working with trigonometric functions. By understanding the basic periods, the impact of transformations, and the method for finding the LCM of periods in combined functions, you'll develop a robust ability to accurately determine the period of a wide variety of trigonometric equations. Remember to always check your work using graphical methods for verification and to avoid common pitfalls. Mastering this skill is essential for solving complex trigonometric problems, understanding their graphical representations, and applying trigonometry to real-world scenarios.
Latest Posts
Latest Posts
-
What Is The Perimeter Of A Parallelogram
Apr 03, 2025
-
Can A Pure Substance Be Separated By Physical Means
Apr 03, 2025
-
Does A Ribosome Have A Membrane
Apr 03, 2025
-
Is Aluminium A Conductor Of Electricity
Apr 03, 2025
-
A Quadrilateral In Which The Diagonals Bisect Each Other
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How To Find Period Of A Trig Eqn . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
