A Quadrilateral In Which The Diagonals Bisect Each Other
Juapaving
Apr 03, 2025 · 5 min read
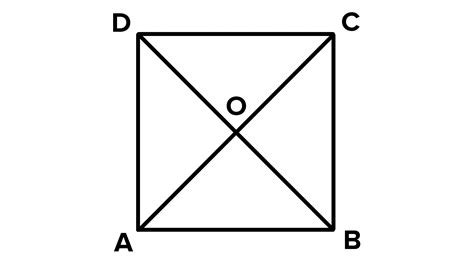
Table of Contents
A Quadrilateral in Which the Diagonals Bisect Each Other: Exploring Parallelograms
A quadrilateral is a polygon with four sides, four vertices, and four angles. Many different types of quadrilaterals exist, each with its unique properties. One particularly interesting class of quadrilaterals are those in which the diagonals bisect each other. This property defines a crucial category of quadrilaterals: parallelograms. This article will delve deep into the characteristics of such quadrilaterals, exploring their properties, theorems, and applications.
Understanding Diagonals and Their Bisection
Before we dive into the specifics of quadrilaterals with bisecting diagonals, let's clarify what we mean by "diagonals" and "bisecting."
-
Diagonals: In a quadrilateral ABCD, the diagonals are the line segments connecting non-adjacent vertices. In other words, AC and BD are the diagonals.
-
Bisecting: To bisect something means to divide it into two equal parts. If the diagonals of a quadrilateral bisect each other, then the point of intersection divides each diagonal into two segments of equal length. This means that in quadrilateral ABCD, if diagonals AC and BD intersect at point O, then AO = OC and BO = OD.
The Defining Characteristic: Parallelograms
The fundamental theorem related to quadrilaterals with bisecting diagonals states:
Theorem: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
This theorem is crucial because it establishes a direct link between the property of bisecting diagonals and the specific type of quadrilateral: a parallelogram. This means that if you observe a quadrilateral where the diagonals cut each other exactly in half, you can immediately classify it as a parallelogram. This simplification streamlines geometric problem-solving.
Properties of Parallelograms
Parallelograms possess several distinct properties, all stemming from the fact that their diagonals bisect each other. These properties are essential for understanding and working with parallelograms in various mathematical contexts:
-
Opposite sides are parallel: This is the defining characteristic of a parallelogram. If we have sides AB and CD, and sides BC and AD, then AB || CD and BC || AD. This parallelism is a direct consequence of the bisecting diagonals.
-
Opposite sides are equal in length: The lengths of opposite sides are equal. Therefore, AB = CD and BC = AD. This property arises from the fact that the diagonals create congruent triangles within the parallelogram.
-
Opposite angles are equal: Opposite angles within a parallelogram have equal measures. Angle A = Angle C and Angle B = Angle D. This equality is a result of the parallel sides and the alternate interior angles theorem.
-
Consecutive angles are supplementary: Consecutive angles (angles that share a side) add up to 180 degrees. Angle A + Angle B = 180°, Angle B + Angle C = 180°, Angle C + Angle D = 180°, and Angle D + Angle A = 180°. This is a consequence of the parallel sides and the same-side interior angles theorem.
-
Diagonals bisect each other: As we've already established, this is the property that leads to the parallelogram classification.
Proof of the Theorem: Diagonals Bisecting Implies Parallelogram
Let's formally prove the theorem that states if the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
Given: Quadrilateral ABCD with diagonals AC and BD intersecting at point O such that AO = OC and BO = OD.
To Prove: ABCD is a parallelogram.
Proof:
-
Consider triangles ΔAOB and ΔCOD: We have AO = OC and BO = OD (given). Also, ∠AOB = ∠COD (vertical angles are equal). Therefore, ΔAOB ≅ ΔCOD (SAS congruence).
-
Congruent Sides: From the congruence of the triangles, we can conclude that AB = CD.
-
Consider triangles ΔBOC and ΔDOA: Similarly, we have BO = OD and OC = OA (given). Also, ∠BOC = ∠DOA (vertical angles are equal). Therefore, ΔBOC ≅ ΔDOA (SAS congruence).
-
Congruent Sides: From the congruence of these triangles, we get BC = AD.
-
Parallel Sides: Since AB = CD and BC = AD (from steps 2 and 4), and the alternate interior angles formed by the intersecting diagonals are equal due to the congruent triangles, we can conclude that AB || CD and BC || AD.
-
Parallelogram: Because opposite sides are parallel (AB || CD and BC || AD), quadrilateral ABCD is a parallelogram.
This proof rigorously establishes the connection between bisecting diagonals and the parallelogram classification.
Special Cases of Parallelograms
Several special cases of parallelograms exist, each with additional properties:
-
Rectangles: A rectangle is a parallelogram with four right angles (90° angles). Its diagonals are equal in length.
-
Rhombuses: A rhombus is a parallelogram with all four sides equal in length. Its diagonals are perpendicular bisectors of each other.
-
Squares: A square is a parallelogram that is both a rectangle and a rhombus. It possesses all the properties of both rectangles and rhombuses.
Applications of Parallelograms
The properties of parallelograms, stemming from their bisecting diagonals, find numerous applications in various fields:
-
Engineering and Architecture: Parallelograms are used in structural design, especially in frameworks and trusses, due to their stability and strength. Understanding their properties is crucial for calculating forces and stresses.
-
Physics: Parallelograms are applied in vector addition and resolution. The parallelogram law of vector addition utilizes the parallelogram's properties to determine the resultant vector of two given vectors.
-
Computer Graphics: Parallelograms play a role in computer graphics transformations, particularly in shearing and scaling operations.
-
Tessellations: Parallelograms are frequently used to create tessellations, repeating patterns that cover a plane without gaps or overlaps.
Beyond Parallelograms: Other Quadrilaterals
While the bisecting diagonals property uniquely identifies parallelograms, it's important to note that other quadrilaterals might exhibit some related properties:
-
Isosceles Trapezoids: An isosceles trapezoid has one pair of parallel sides and equal non-parallel sides. While its diagonals don't necessarily bisect each other, they are equal in length.
-
Kites: A kite has two pairs of adjacent sides that are equal in length. The diagonals of a kite are perpendicular, but only one diagonal is bisected by the other.
Conclusion: The Significance of Bisecting Diagonals
The property of having diagonals that bisect each other is a powerful tool in classifying and understanding quadrilaterals. This property directly leads to the identification of parallelograms and their associated characteristics. The implications extend beyond simple geometric classification, impacting fields ranging from engineering and physics to computer graphics and art. A deep understanding of this property allows for efficient problem-solving and unlocks a wealth of geometric insights. The seemingly simple property of bisecting diagonals holds significant weight in the broader world of geometry and its applications. This characteristic serves as a foundational concept for further explorations into the rich world of quadrilaterals and their multifaceted properties.
Latest Posts
Latest Posts
-
Difference Between An Environment And An Ecosystem
Apr 04, 2025
-
What Is The Percent Of 7 25
Apr 04, 2025
-
Common Multiples Of 8 And 9
Apr 04, 2025
-
Reproduction In Most Single Celled Organisms Is Usually Done By Blank
Apr 04, 2025
-
How Many Feet Is A 100 Yards
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about A Quadrilateral In Which The Diagonals Bisect Each Other . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
