How To Find Factors Of Equation
Juapaving
Apr 05, 2025 · 6 min read
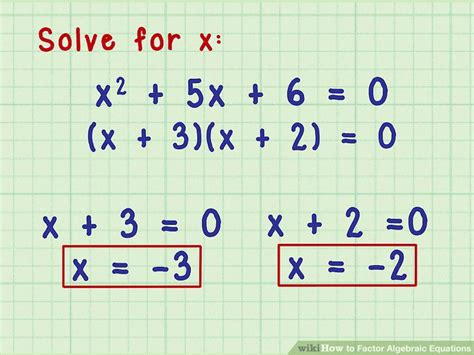
Table of Contents
How to Find Factors of an Equation: A Comprehensive Guide
Finding the factors of an equation is a fundamental skill in algebra and has wide-ranging applications in various fields, from solving complex equations to optimizing engineering designs. This comprehensive guide will walk you through different methods for finding factors, catering to various levels of complexity. We’ll cover techniques applicable to both simple and advanced equations, equipping you with the tools to tackle any factoring challenge.
Understanding Factors and Factorization
Before diving into the methods, let's solidify our understanding of the core concepts. Factors are numbers or expressions that divide another number or expression evenly, leaving no remainder. Factorization, or factoring, is the process of breaking down a mathematical expression into its factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. Similarly, the factors of the expression x² - 4 are (x - 2) and (x + 2) because (x - 2)(x + 2) = x² - 4.
The ability to factor equations is crucial for several reasons:
- Solving Equations: Factoring simplifies equations, often leading to simpler solutions. For example, solving x² - 4 = 0 is much easier after factoring it into (x - 2)(x + 2) = 0.
- Simplifying Expressions: Factoring can significantly simplify complex algebraic expressions, making them easier to understand and manipulate.
- Analyzing Functions: In calculus and other advanced mathematical fields, factoring is essential for analyzing the behavior of functions, identifying critical points, and understanding their properties.
Methods for Finding Factors
The method you choose to find factors depends on the type of equation you’re dealing with. Here are some of the most common techniques:
1. Greatest Common Factor (GCF)
This is the simplest factoring method. It involves identifying the greatest common factor among all terms in the equation and factoring it out.
Example: Factor 3x² + 6x
- Identify the GCF: The GCF of 3x² and 6x is 3x.
- Factor out the GCF: 3x(x + 2)
Therefore, the factors are 3x and (x + 2).
2. Factoring Trinomials (Quadratic Equations)
Trinomials are polynomials with three terms. Factoring trinomials of the form ax² + bx + c requires finding two numbers that add up to 'b' and multiply to 'ac'.
Example: Factor x² + 5x + 6
- Find two numbers that add up to 5 and multiply to 6: These numbers are 2 and 3.
- Rewrite the trinomial: x² + 2x + 3x + 6
- Factor by grouping: x(x + 2) + 3(x + 2)
- Factor out the common binomial: (x + 2)(x + 3)
Therefore, the factors are (x + 2) and (x + 3).
3. Difference of Squares
This method applies to binomials (expressions with two terms) that are the difference of two perfect squares. The formula is: a² - b² = (a + b)(a - b)
Example: Factor x² - 9
- Identify a and b: a = x, b = 3 (since 9 = 3²)
- Apply the formula: (x + 3)(x - 3)
Therefore, the factors are (x + 3) and (x - 3).
4. Sum and Difference of Cubes
These methods are used for factoring expressions that are the sum or difference of two perfect cubes. The formulas are:
- Sum of Cubes: a³ + b³ = (a + b)(a² - ab + b²)
- Difference of Cubes: a³ - b³ = (a - b)(a² + ab + b²)
Example: Factor x³ - 8
- Identify a and b: a = x, b = 2 (since 8 = 2³)
- Apply the difference of cubes formula: (x - 2)(x² + 2x + 4)
Therefore, the factors are (x - 2) and (x² + 2x + 4).
5. Factoring by Grouping
This method is useful for polynomials with four or more terms. It involves grouping terms with common factors and then factoring out those common factors.
Example: Factor 2x³ + 4x² + x + 2
- Group the terms: (2x³ + 4x²) + (x + 2)
- Factor out the common factors from each group: 2x²(x + 2) + 1(x + 2)
- Factor out the common binomial: (x + 2)(2x² + 1)
Therefore, the factors are (x + 2) and (2x² + 1).
6. Quadratic Formula
For quadratic equations (ax² + bx + c = 0) that are difficult or impossible to factor using the methods above, the quadratic formula can be used to find the roots. The roots, also known as zeros or solutions, can then be used to determine the factors. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Once you find the roots (let's call them x₁ and x₂), the factors are (x - x₁) and (x - x₂).
7. Synthetic Division
Synthetic division is a shortcut method for dividing a polynomial by a linear factor (x - c). If the remainder is zero, then (x - c) is a factor. This method is particularly helpful for finding factors of higher-degree polynomials. The process involves a series of additions and multiplications, significantly simplifying the division process.
8. Rational Root Theorem
The rational root theorem helps to identify potential rational roots (roots that are fractions) of a polynomial equation. It states that if a polynomial has a rational root p/q (where p and q are integers and q ≠ 0), then p must be a factor of the constant term, and q must be a factor of the leading coefficient. This narrows down the possibilities for testing potential roots.
Advanced Factoring Techniques
For more complex equations, you might need to employ more advanced techniques, including:
- Partial Fraction Decomposition: This method is used to break down rational functions (fractions with polynomials in the numerator and denominator) into simpler fractions.
- Substitution: Sometimes, substituting a variable with a simpler expression can simplify the equation and make it easier to factor.
- Using Technology: Computer algebra systems (CAS) and online calculators can help factor complex polynomials quickly and efficiently.
Practical Applications of Factoring
The ability to factor equations is crucial in various fields:
- Engineering: In structural analysis and design, factoring is used to solve equations related to stress, strain, and deflection.
- Physics: Many physics problems involve solving equations to determine variables such as velocity, acceleration, and force.
- Economics: Economic models often involve equations that need to be factored to analyze market behavior and predict trends.
- Computer Science: Factoring is used in cryptography and algorithm design.
Conclusion
Mastering factoring techniques is essential for success in algebra and various other fields. From the basic GCF method to the more advanced techniques like synthetic division and the rational root theorem, choosing the right approach depends on the specific equation you are working with. Practice is key to developing proficiency. The more you practice, the quicker and more confidently you’ll be able to identify and apply the appropriate factoring method to solve any equation you encounter. Remember to always check your work by expanding the factored form to ensure it matches the original equation. By understanding and applying these methods, you’ll unlock a crucial skill that will serve you well in your mathematical endeavors.
Latest Posts
Latest Posts
-
What Is 104 Fahrenheit In Celsius
Apr 05, 2025
-
201 In Roman Numerals Crossword Clue
Apr 05, 2025
-
What Is A Major Element Found In Chlorophyll
Apr 05, 2025
-
Boiling Water Is A Chemical Or Physical Change
Apr 05, 2025
-
All Real Numbers On A Number Line
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about How To Find Factors Of Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
