All Real Numbers On A Number Line
Juapaving
Apr 05, 2025 · 6 min read
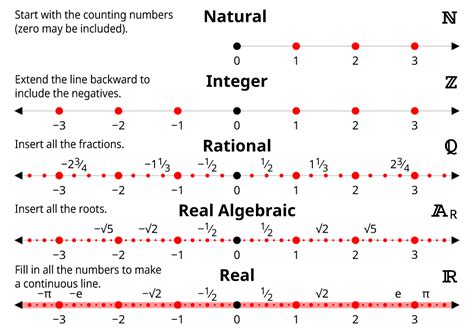
Table of Contents
All Real Numbers on a Number Line: A Comprehensive Guide
The number line, a seemingly simple visual tool, is fundamental to understanding mathematics. It provides a concrete representation of the abstract concept of real numbers, allowing us to visualize their relationships, order, and operations. This article delves into the comprehensive world of real numbers and their representation on the number line, exploring various aspects from basic concepts to more advanced topics.
What are Real Numbers?
Real numbers encompass all the numbers we typically encounter in everyday life and most mathematical applications. They can be broadly categorized into several sets:
1. Natural Numbers (Counting Numbers):
These are the positive whole numbers starting from 1: 1, 2, 3, 4, 5,... They are used for counting discrete objects. On the number line, they are represented as equally spaced points to the right of zero.
2. Whole Numbers:
This set includes natural numbers and zero: 0, 1, 2, 3, 4, 5,... The addition of zero provides a starting point for the number line.
3. Integers:
Integers comprise whole numbers and their negative counterparts: ..., -3, -2, -1, 0, 1, 2, 3,... They extend the number line to the left of zero, representing values less than zero.
4. Rational Numbers:
Rational numbers can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. Examples include 1/2, -3/4, 0, 2, -5. These numbers can be precisely located on the number line. They either terminate (e.g., 1/4 = 0.25) or repeat (e.g., 1/3 = 0.333...).
5. Irrational Numbers:
These numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include:
- π (pi): Approximately 3.14159..., representing the ratio of a circle's circumference to its diameter.
- e (Euler's number): Approximately 2.71828..., the base of the natural logarithm.
- √2 (the square root of 2): Approximately 1.41421..., a number whose square is 2.
Irrational numbers fill in the gaps between rational numbers on the number line, ensuring that the line is completely "full."
6. Real Numbers:
The union of rational and irrational numbers forms the set of real numbers. This comprehensive set includes all the numbers mentioned above, encompassing every point on the number line. There are no "holes" or gaps in the real number line. Every point corresponds to a unique real number, and every real number corresponds to a unique point.
Visualizing Real Numbers on the Number Line
The number line is a horizontal line extending infinitely in both directions. A central point, marked as 0 (zero), serves as the origin. Positive numbers are located to the right of zero, and negative numbers are located to the left. The distance between consecutive integers represents a unit length, providing a scale for measuring distances and comparing magnitudes.
Representing Different Number Types:
- Integers: Integers are easily marked as distinct points on the number line.
- Rational Numbers: Rational numbers can be accurately plotted by dividing the unit length into appropriate fractions.
- Irrational Numbers: While we cannot precisely mark irrational numbers due to their non-terminating decimal expansions, we can approximate their positions based on their decimal values. For example, we can approximate π as being slightly greater than 3.14.
Ordering and Comparing Real Numbers:
The number line facilitates the ordering and comparison of real numbers. A number is considered greater than another if it lies to the right of it on the number line. Conversely, a number is less than another if it lies to the left. This ordering provides a clear visual representation of inequalities.
Advanced Concepts and Applications
The number line's simplicity belies its power in tackling complex mathematical concepts.
1. Intervals and Inequalities:
The number line is crucial for representing intervals and inequalities. Intervals represent sets of real numbers within a specific range. They can be open (excluding endpoints), closed (including endpoints), or half-open/half-closed. For example:
- (a, b): Open interval, representing all real numbers x such that a < x < b.
- [a, b]: Closed interval, representing all real numbers x such that a ≤ x ≤ b.
- [a, b): Half-open interval, representing all real numbers x such that a ≤ x < b.
These intervals can be readily visualized and understood using the number line.
2. Absolute Value:
The absolute value of a real number is its distance from zero on the number line. It is always non-negative. The number line helps in visualizing and understanding the geometric interpretation of absolute value.
3. Functions and Graphs:
The number line is often used as the domain (input values) axis when graphing functions of a single variable. The range (output values) is typically represented on a vertical number line (y-axis). The combination of both creates the Cartesian coordinate system.
4. Limits and Continuity:
In calculus, the number line plays a vital role in understanding limits and continuity of functions. Limits describe the behavior of a function as its input approaches a specific value. The number line helps to visualize the approach and the limiting value.
5. Sequences and Series:
The number line can be used to visualize sequences and series. A sequence is an ordered list of numbers, which can be represented as points on the number line. The convergence or divergence of a series can also be illustrated graphically.
Density of Real Numbers
A remarkable property of real numbers is their density. Between any two distinct real numbers, no matter how close, there always exists another real number. This implies an infinite number of real numbers between any two given real numbers. This property is a consequence of the completeness property of real numbers, which states that every bounded set of real numbers has a least upper bound and a greatest lower bound.
This density is visually represented on the number line: you can always find another point between any two existing points. This infinite density underscores the richness and complexity of the real number system.
The Completeness Property and the Real Number Line
The completeness property is a fundamental characteristic distinguishing the real numbers from the rational numbers. It ensures that the real number line is continuous, without any "holes" or gaps. This property is crucial for various mathematical theorems and applications, particularly in calculus and analysis.
The completeness property guarantees the existence of solutions to equations that might not have rational solutions. For example, the equation x² = 2 has no rational solution, but it has a real solution (√2), which is an irrational number. The existence of this solution is guaranteed by the completeness property.
Conclusion: The Number Line's Enduring Importance
The number line, despite its apparent simplicity, is an indispensable tool in mathematics. It provides a concrete representation of abstract concepts, allowing for a deeper understanding of real numbers, their properties, and their relationships. From basic arithmetic operations to advanced calculus concepts, the number line's visual power continues to illuminate the world of mathematics, offering a profound insight into the intricacies of the real number system. Its ability to visualize ordering, inequalities, intervals, limits, and other key mathematical ideas makes it an essential tool for students and mathematicians alike. The seemingly simple line embodies the richness and complexity of the mathematical universe. Understanding the real numbers and their representation on the number line forms a crucial foundation for further mathematical explorations.
Latest Posts
Related Post
Thank you for visiting our website which covers about All Real Numbers On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
