Least Common Multiple Of 3 4 And 9
Juapaving
Apr 06, 2025 · 5 min read
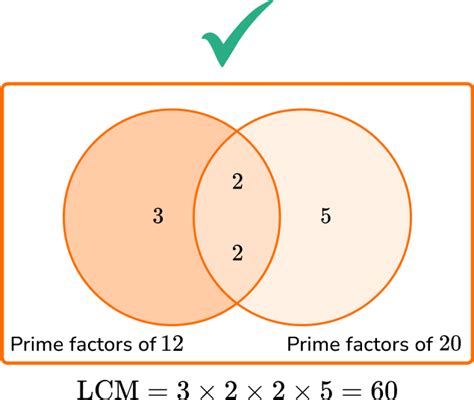
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 4, and 9: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, ranging from simplifying fractions to solving complex algebraic problems. This article delves into the process of calculating the LCM of 3, 4, and 9, providing multiple methods and exploring the underlying mathematical principles. We will also examine the broader significance of the LCM and its practical uses.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer that is divisible by both 2 and 3.
Methods for Calculating the LCM of 3, 4, and 9
There are several effective methods for determining the LCM of a set of numbers. Let's explore the most common approaches, applying them to find the LCM of 3, 4, and 9.
1. Listing Multiples Method
This method involves listing the multiples of each number until you find the smallest multiple common to all.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36...
- Multiples of 9: 9, 18, 27, 36...
By comparing the lists, we can see that the smallest common multiple is 36. Therefore, the LCM(3, 4, 9) = 36. This method is straightforward for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization of a number is expressing it as a product of its prime factors.
- Prime factorization of 3: 3
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization:
- Identify all the prime factors: In this case, the prime factors are 2 and 3.
- Select the highest power of each prime factor: The highest power of 2 is 2², and the highest power of 3 is 3².
- Multiply the selected powers: 2² x 3² = 4 x 9 = 36
Therefore, the LCM(3, 4, 9) = 36. This method is generally more efficient for larger numbers than the listing multiples method.
3. Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides all the given numbers without leaving a remainder. There's a formula that connects the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
This can be extended to more than two numbers, though the calculation becomes more complex. Let's first find the GCD of 3, 4, and 9. Since 3, 4, and 9 don't share any common factors other than 1, their GCD is 1.
However, applying this formula directly to three numbers requires a slightly modified approach. We can find the LCM of 3 and 4, then find the LCM of that result and 9.
- LCM(3, 4) = 12 (using prime factorization or listing multiples)
- LCM(12, 9) = 36 (using prime factorization or listing multiples)
Therefore, LCM(3, 4, 9) = 36. While this method works, prime factorization remains generally more efficient for multiple numbers.
Practical Applications of LCM
The concept of the least common multiple has numerous applications in various fields:
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential for finding a common denominator.
-
Scheduling Problems: The LCM is used to solve scheduling problems, such as determining when events will occur simultaneously. For example, if one event happens every 3 days, another every 4 days, and a third every 9 days, the LCM (3, 4, 9) = 36 will tell you that all three events will coincide every 36 days.
-
Gear Ratios and Rotational Speeds: In mechanical engineering, the LCM helps determine the synchronization of rotating gears or shafts with different speeds.
-
Cyclic Processes: In various scientific and engineering contexts involving cyclical processes (e.g., oscillations, periodic signals), the LCM helps determine when cycles align or repeat.
-
Music Theory: The LCM plays a role in understanding musical intervals and harmonies.
Further Exploration of LCM Concepts
LCM and GCD Relationship
As mentioned earlier, the LCM and GCD are intrinsically linked. For two integers 'a' and 'b':
LCM(a, b) * GCD(a, b) = a * b
This relationship provides an alternative method for calculating the LCM if the GCD is known.
Euclidean Algorithm for GCD
The Euclidean algorithm is an efficient method for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is zero. The last non-zero remainder is the GCD.
LCM of More Than Three Numbers
The methods described earlier can be extended to find the LCM of more than three numbers. The prime factorization method remains particularly efficient for this purpose. You would identify all prime factors across all the numbers, select the highest power of each, and then multiply them together.
LCM and Computer Science
The LCM plays a role in various computer science algorithms and data structures. For example, it's used in optimizing memory allocation and managing concurrent processes.
Conclusion
Finding the least common multiple is a fundamental skill with wide-ranging applications. While the listing multiples method is intuitive for smaller numbers, the prime factorization method is generally more efficient and scalable for larger sets of numbers. Understanding the relationship between the LCM and GCD provides additional tools for solving these types of problems. Mastering the LCM enhances one's mathematical skills and opens doors to solving a broader array of problems in various fields. The LCM of 3, 4, and 9, as demonstrated through various methods, is definitively 36. This knowledge provides a solid foundation for tackling more complex LCM calculations and their real-world applications.
Latest Posts
Latest Posts
-
Bromine Has How Many Valence Electrons
Apr 09, 2025
-
Fluid Pressure Against A Wall Or Cell Membranes Is Called
Apr 09, 2025
-
What Is The Largest Cell Called
Apr 09, 2025
-
Conventional And Non Conventional Energy Sources
Apr 09, 2025
-
The Energy In Motion Is Called
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 3 4 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.