How To Calculate Tension In A Cable
Juapaving
Mar 31, 2025 · 6 min read
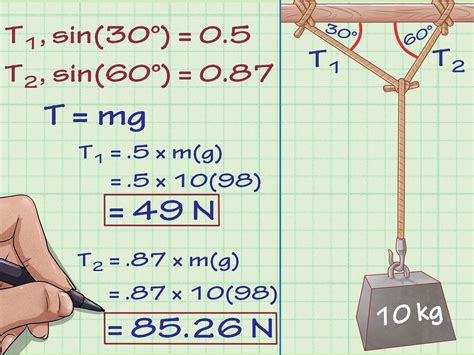
Table of Contents
How to Calculate Tension in a Cable: A Comprehensive Guide
Calculating cable tension is a crucial aspect of engineering, physics, and various practical applications. From designing suspension bridges to understanding forces in pulley systems, accurately determining cable tension ensures structural integrity and operational safety. This comprehensive guide delves into the different methods and scenarios involved in calculating cable tension, providing you with the knowledge and tools to tackle a range of problems.
Understanding the Basics: Forces and Equilibrium
Before diving into calculations, let's establish a foundational understanding of the key principles at play. Cable tension arises from the internal forces within a cable resisting an external load. This internal force acts along the length of the cable, pulling equally in both directions. Crucially, when a cable is in static equilibrium (not accelerating), the net force acting on it is zero. This principle, known as Newton's First Law of Motion, forms the basis of our calculations.
Key Concepts:
- Force: A vector quantity representing an interaction that can change the motion of an object. Measured in Newtons (N).
- Tension: The pulling force transmitted through a cable or rope. It's always directed along the cable's length.
- Equilibrium: A state where the net force and net torque acting on an object are both zero. This means the object is either at rest or moving at a constant velocity.
- Free Body Diagram (FBD): A visual representation of an object showing all the forces acting on it. Creating a FBD is essential for solving tension problems.
Methods for Calculating Cable Tension
The method used to calculate cable tension depends heavily on the specific arrangement of the system. We'll explore several common scenarios:
1. Simple Cable with a Single Load
This is the simplest scenario: a cable supporting a single weight hanging vertically. In this case, the tension in the cable is equal to the weight of the object.
Example: A 10 kg weight hangs from a cable. The tension (T) in the cable is:
T = mg = (10 kg)(9.81 m/s²) = 98.1 N
Where:
- m = mass of the object
- g = acceleration due to gravity (approximately 9.81 m/s²)
2. Cable Supported at Two Points with a Single Load
This scenario involves a cable supported at two points, with a weight hanging somewhere along its length. The tension in the cable is not uniform throughout its length and will be different in each section. To solve this, we use trigonometry and resolve forces in the horizontal and vertical directions.
Example: Consider a cable of length L, supported at points A and B, with a weight W hanging at point C. The angles formed by the cable segments AC and BC with the horizontal are θ₁ and θ₂, respectively. We can resolve the forces:
- Vertical Equilibrium: T₁sin(θ₁) + T₂sin(θ₂) = W
- Horizontal Equilibrium: T₁cos(θ₁) = T₂cos(θ₂)
Solving these two equations simultaneously allows us to find T₁ and T₂ (the tensions in cable segments AC and BC).
Important Note: The angles θ₁ and θ₂ are crucial for accurate calculations. Measuring or calculating these angles precisely is vital.
3. Cable with Multiple Loads
When multiple loads are supported by a cable, the tension varies along the cable's length. Each section of the cable between loads must be considered separately. We can use a similar approach as in the previous scenario, applying equilibrium conditions to each section. This often involves creating multiple free body diagrams, one for each section.
Example: Imagine a cable supporting three weights, W₁, W₂, and W₃, at different points. To find the tension in the cable segments between each weight, you'd need to analyze each section independently, applying the equilibrium equations. This will typically involve a system of multiple equations that need to be solved simultaneously.
4. Inclined Cable with a Single Load
If the cable is inclined at an angle, the tension will be greater than the weight of the load. This is because the tension must have a component to support the load's weight vertically, and another component to balance the horizontal component of the force. Again, resolving forces in the horizontal and vertical directions is essential.
Example: Consider a cable inclined at an angle α supporting a weight W. The tension T can be found by:
- Vertical Equilibrium: Tsin(α) = W
- Therefore, T = W/sin(α)
This shows that as the angle α decreases (cable becomes more horizontal), the tension increases significantly.
5. Cables in Pulley Systems
Pulley systems involve cables wrapped around pulleys to change the direction or magnitude of the force. The tension in the cable will be affected by the number of pulleys and the system's configuration. In ideal scenarios (frictionless pulleys and massless cables), the tension is uniform throughout the cable. However, in real-world scenarios, friction and pulley mass must be considered, making the calculations more complex.
Example: A simple pulley system with a single pulley doubles the mechanical advantage. If a weight W is lifted using a rope and a single pulley, the tension in the rope is W/2 (assuming frictionless pulley).
Advanced Considerations:
1. Cable Sag and Catenery Curves:
In many real-world situations, cables sag under their own weight and the loads they carry. This sag creates a catenary curve, which is a more complex shape than a straight line. Calculating the tension in a sagging cable requires more advanced techniques, often involving calculus and differential equations. Approximate solutions are often used for engineering purposes.
2. Cable Material Properties:
The material properties of the cable, such as its elasticity (Young's Modulus), influence the tension. A more elastic cable will stretch more under load, affecting the tension distribution. These effects are considered in more advanced calculations involving stress and strain.
3. Wind Loads and Other External Forces:
External factors like wind loads significantly affect cable tension. These forces must be incorporated into the calculations. The wind load depends on the cable's geometry, the wind speed, and the cable's surface area.
4. Dynamic Loads:
The analysis of cable tension becomes more complex under dynamic loads (time-varying forces). In such cases, the principles of dynamics and differential equations are essential for accurately determining tension.
Practical Applications and Examples:
Calculating cable tension finds applications across diverse fields:
- Civil Engineering: Designing suspension bridges, cable-stayed bridges, and tensioned structures.
- Mechanical Engineering: Analyzing cranes, lifting equipment, and conveyor belts.
- Electrical Engineering: Designing overhead power lines and transmission cables.
- Marine Engineering: Calculating tension in mooring lines and ship rigging.
Example: Suspension Bridge Design: In designing a suspension bridge, engineers must carefully calculate the tension in the main cables to ensure they can support the weight of the bridge deck and traffic loads. This involves sophisticated modeling and analysis, accounting for cable sag, wind loads, and other external factors.
Example: Crane Operation: Understanding cable tension is crucial for safe crane operation. The tension in the hoisting cable must be sufficient to lift the load but not so high as to exceed the cable's strength.
Conclusion:
Calculating cable tension accurately is vital across numerous engineering and physical applications. While simple scenarios can be solved using basic trigonometry and equilibrium principles, more complex situations require advanced techniques and considerations such as sag, material properties, and dynamic loads. Understanding the fundamental principles and applying the appropriate methods are critical for ensuring structural integrity, operational safety, and the successful design and operation of various systems involving cables. This guide provides a solid foundation for tackling a wide range of cable tension problems, from simple scenarios to more challenging, real-world applications. Remember to always consult relevant engineering standards and codes of practice when dealing with real-world applications.
Latest Posts
Latest Posts
-
A Tetrad Is Made Up Of
Apr 02, 2025
-
What Is A Single Celled Organism
Apr 02, 2025
-
If Diagonals Of A Quadrilateral Bisect Each Other
Apr 02, 2025
-
Is Pure Water A Mixture Or Compound
Apr 02, 2025
-
What Type Of Device Is A Keyboard
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Calculate Tension In A Cable . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
