How To Calculate A Perimeter Of A Triangle
Juapaving
Apr 05, 2025 · 5 min read
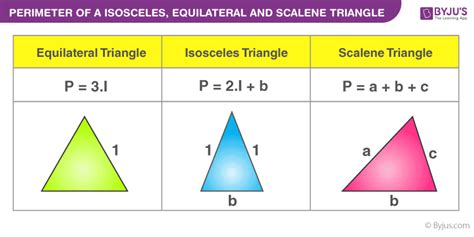
Table of Contents
How to Calculate the Perimeter of a Triangle: A Comprehensive Guide
The perimeter of any shape is the total distance around its exterior. For triangles, this means adding the lengths of all three sides. While seemingly straightforward, understanding how to calculate a triangle's perimeter encompasses various scenarios and requires familiarity with different triangle types and properties. This comprehensive guide will walk you through every aspect of calculating a triangle's perimeter, from simple examples to more complex scenarios involving various geometric principles.
Understanding Triangles: Types and Properties
Before diving into perimeter calculations, let's briefly review the different types of triangles and their properties. This knowledge will be crucial in determining the most efficient method for calculating the perimeter.
Types of Triangles Based on Sides:
- Equilateral Triangle: All three sides are equal in length.
- Isosceles Triangle: Two sides are equal in length.
- Scalene Triangle: All three sides have different lengths.
Types of Triangles Based on Angles:
- Acute Triangle: All angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
Understanding these classifications helps anticipate the information required for perimeter calculation. For example, knowing a triangle is equilateral means you only need the length of one side to calculate the perimeter.
Calculating the Perimeter: Simple Scenarios
The most fundamental method for calculating a triangle's perimeter is simply adding the lengths of its three sides. Let's illustrate this with a few examples.
Example 1: A Simple Scalene Triangle
Imagine a triangle with sides measuring 5 cm, 7 cm, and 9 cm. To find the perimeter (P), we simply add the lengths of these sides:
P = 5 cm + 7 cm + 9 cm = 21 cm
Therefore, the perimeter of this scalene triangle is 21 cm.
Example 2: An Equilateral Triangle
Consider an equilateral triangle with a side length of 6 inches. Since all sides are equal, the perimeter is:
P = 6 inches + 6 inches + 6 inches = 18 inches
or, more efficiently:
P = 3 * 6 inches = 18 inches
Example 3: An Isosceles Triangle
Let's say we have an isosceles triangle with two equal sides of 4 cm each and a third side of 6 cm. The perimeter is:
P = 4 cm + 4 cm + 6 cm = 14 cm
Calculating the Perimeter: More Complex Scenarios
In some cases, you might not be given the lengths of all three sides directly. You may need to utilize other information and geometric principles to find the missing side lengths before calculating the perimeter.
Using the Pythagorean Theorem (Right Triangles)
The Pythagorean theorem is a fundamental concept in geometry, especially useful when dealing with right-angled triangles. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs or cathetus).
a² + b² = c²
where:
- 'a' and 'b' are the lengths of the two shorter sides (legs).
- 'c' is the length of the hypotenuse.
Once you've calculated the length of the missing side using the Pythagorean theorem, you can then proceed to calculate the perimeter by adding all three sides.
Example 4: A Right-Angled Triangle
Let's say we have a right-angled triangle with one leg of 3 cm and another leg of 4 cm. To find the hypotenuse (c), we apply the Pythagorean theorem:
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25 = 5 cm
Now that we have all three side lengths (3 cm, 4 cm, and 5 cm), we can calculate the perimeter:
P = 3 cm + 4 cm + 5 cm = 12 cm
Using Heron's Formula (Any Triangle)
Heron's formula allows us to calculate the area of a triangle if we know the lengths of all three sides. While not directly used for perimeter calculation, it's indirectly helpful as it allows the calculation of the triangle's area which is sometimes used to solve for missing side lengths within a problem.
Heron's formula states:
Area = √(s(s-a)(s-b)(s-c))
where:
- 'a', 'b', and 'c' are the lengths of the three sides.
- 's' is the semi-perimeter, calculated as s = (a + b + c) / 2
Example 5: Using Heron's Formula to indirectly find the perimeter
Suppose you know the area of a triangle (let's say 6 square cm) and two of its sides, 4 cm and 5 cm. You can use Heron's formula to indirectly calculate the perimeter.
You can’t directly find the third side, but you can iteratively test values of the third side to see what yields the correct area. While not very practical for hand calculations, this is useful for computational approaches. Once the third side is found, simply sum all sides to find the perimeter.
Advanced Techniques and Applications
The calculation of the triangle's perimeter can be integrated into various real-world applications and more advanced mathematical concepts.
Trigonometry and Perimeter Calculations
Trigonometric functions (sine, cosine, tangent) can be employed when you only have partial information about the triangle, such as an angle and the length of one side. Using trigonometric ratios, you can calculate the remaining side lengths and subsequently the perimeter.
Perimeter and Area Relationships
While perimeter and area are distinct concepts, they are related. Understanding this relationship can help in solving certain geometric problems. For instance, for a given perimeter, there is a triangle with the maximum possible area (an equilateral triangle). Conversely, for a given area, there are many possible perimeters, with the equilateral triangle usually having the smallest.
Applications in Real-World Scenarios
Perimeter calculations have applications in various fields, including:
- Construction: Determining the amount of fencing needed for a triangular plot of land.
- Engineering: Calculating the length of materials required for structural frameworks.
- Cartography: Measuring distances between points on a map represented by triangles.
- Computer Graphics: Creating and manipulating triangular meshes in 3D modeling.
Conclusion: Mastering Triangle Perimeter Calculations
Calculating the perimeter of a triangle is a foundational concept in geometry with wide-ranging applications. While the basic method involves simply adding the lengths of the three sides, understanding different triangle types and employing techniques such as the Pythagorean theorem and Heron's formula allows for the efficient calculation of perimeters in more complex scenarios. Mastering these methods opens doors to solving intricate geometric problems and applying this knowledge to various real-world situations. Remember to always carefully consider the given information, choose the appropriate method, and double-check your calculations for accuracy.
Latest Posts
Latest Posts
-
2nd Highest Civilian Award In India
Apr 05, 2025
-
Coefficient Of X M X M
Apr 05, 2025
-
Transverse Waves Are Mechanical Or Non Mechanical
Apr 05, 2025
-
Are Angles Whose Measures Have A Sum Of 90 Degrees
Apr 05, 2025
-
Does A Rhombus Have Point Symmetry
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about How To Calculate A Perimeter Of A Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
