Does A Rhombus Have Point Symmetry
Juapaving
Apr 05, 2025 · 5 min read
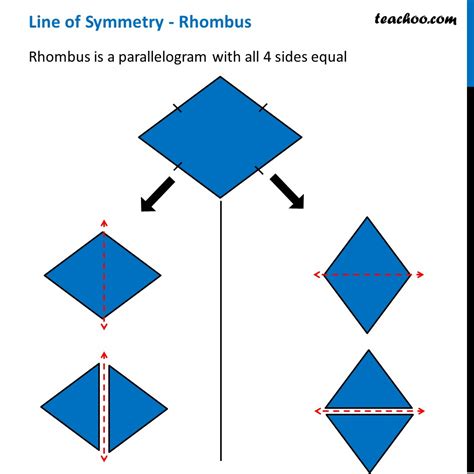
Table of Contents
Does a Rhombus Have Point Symmetry? A Comprehensive Exploration
Point symmetry, also known as central symmetry, is a fascinating concept in geometry. It describes a figure that can be rotated 180 degrees about a central point and still appear unchanged. This central point is called the center of symmetry. But does this property hold true for all quadrilaterals, specifically, the rhombus? This article will delve deep into the characteristics of a rhombus, explore the concept of point symmetry, and ultimately answer the question: Does a rhombus possess point symmetry?
Understanding the Rhombus: A Geometric Overview
Before we delve into the intricacies of point symmetry, let's refresh our understanding of a rhombus. A rhombus is a special type of quadrilateral defined by its unique properties:
- Four equal sides: All four sides of a rhombus are congruent (equal in length).
- Opposite sides are parallel: Opposite sides of a rhombus are parallel to each other. This makes it a parallelogram.
- Opposite angles are equal: The angles opposite each other in a rhombus are congruent.
- Consecutive angles are supplementary: Any two angles adjacent to each other add up to 180 degrees.
- Diagonals bisect each other at right angles: The diagonals of a rhombus intersect at a point, dividing each other into two equal segments, and forming four right angles at the intersection.
These defining characteristics are crucial in determining whether a rhombus possesses point symmetry. Understanding these properties will pave the way for a clearer understanding of the symmetry properties of a rhombus.
Delving into Point Symmetry: A Definition and Examples
Point symmetry, as mentioned earlier, describes an object that remains unchanged after a 180-degree rotation around a central point. This central point serves as the point of symmetry. To visualize this, imagine folding a figure along a line passing through the center of symmetry. If the two halves perfectly overlap, the figure has point symmetry.
Let's consider some examples:
-
A square: A square possesses point symmetry. The center of the square is the point of symmetry. If you rotate a square 180 degrees around its center, it will look exactly the same.
-
A rectangle: A rectangle also exhibits point symmetry. The center of the rectangle acts as the point of symmetry. Rotating it 180 degrees about this point leaves the rectangle unchanged.
-
A circle: A circle has infinite point symmetry. Every point in the circle could be considered a point of symmetry as a 180 degree rotation about any point would produce an identical circle.
These examples illustrate the concept of point symmetry. Now, let's apply this understanding to the rhombus to determine if it holds this property.
Investigating the Point Symmetry of a Rhombus
To determine if a rhombus has point symmetry, we need to consider the implications of rotating it 180 degrees about a potential center of symmetry. The most likely candidate for this center is the intersection point of the diagonals. This point is also the centroid of the rhombus.
Let's analyze the impact of a 180-degree rotation around the intersection point of the diagonals:
-
Rotation of the vertices: Each vertex of the rhombus will rotate 180 degrees around the center. This rotation will map each vertex onto its opposite vertex. This ensures that the shape remains unchanged after the rotation.
-
Rotation of the sides: Each side of the rhombus will rotate 180 degrees. After rotation, each side will occupy the position of its opposite side. Again, the shape remains identical.
-
Rotation of the angles: Similarly, each angle will rotate 180 degrees, mapping onto its opposite angle. Since opposite angles in a rhombus are equal, the resulting shape is congruent to the original.
Based on this analysis, we can conclude that a 180-degree rotation of a rhombus about the intersection point of its diagonals results in a figure that is identical to the original. This unequivocally demonstrates that:
A rhombus possesses point symmetry.
Rhombus vs. Other Quadrilaterals: A Comparative Analysis of Symmetry
Comparing the symmetry of a rhombus to other quadrilaterals provides a deeper understanding of its unique geometric properties. Let's examine the symmetry characteristics of some related quadrilaterals:
-
Square: A square has both point symmetry and line symmetry (multiple lines of symmetry). It's highly symmetrical.
-
Rectangle: A rectangle, like the rhombus, possesses point symmetry. It also has two lines of symmetry.
-
Parallelogram: A parallelogram generally has point symmetry if it is a rectangle or a rhombus. However, a general parallelogram that does not fulfill these conditions lacks point symmetry.
-
Trapezoid: A trapezoid typically lacks both point symmetry and line symmetry. The exceptions are isosceles trapezoids which can possess one or two lines of symmetry but will not have point symmetry.
-
Kite: A kite generally does not possess point symmetry, however it can have one line of symmetry.
This comparison highlights that while a rhombus shares point symmetry with squares and rectangles, it differs from other quadrilaterals in its specific symmetry properties.
Applications of Point Symmetry in Real-World Scenarios
The concept of point symmetry, while seemingly abstract, has practical applications in various fields:
-
Art and Design: Artists and designers utilize point symmetry to create aesthetically pleasing and balanced compositions. Many logos and patterns exhibit point symmetry.
-
Architecture: Architects often incorporate point symmetry in building designs to achieve visual harmony and structural stability. Many buildings and structures display elements of point symmetry.
-
Engineering: Engineers use the principles of symmetry, including point symmetry, in designing various structures and mechanisms to ensure stability and functionality. The concept is important for balance and efficient load distribution.
-
Nature: Point symmetry can be observed in many natural phenomena, such as snowflakes and certain types of flowers. These examples illustrate the widespread occurrence of point symmetry in the natural world.
Conclusion: A Definitive Answer on Rhombus Point Symmetry
In conclusion, the question of whether a rhombus possesses point symmetry receives a resounding yes. The intersection of its diagonals serves as the center of symmetry, and a 180-degree rotation around this point leaves the rhombus unchanged. This property, shared with squares and rectangles, distinguishes the rhombus within the broader category of quadrilaterals and showcases its unique geometric characteristics. Understanding point symmetry and its presence in a rhombus adds to a deeper comprehension of geometrical concepts and their applications in various fields. The implications extend beyond theoretical geometry, impacting real-world applications in art, architecture, engineering, and nature.
Latest Posts
Latest Posts
-
What Are The Factors Of 117
Apr 06, 2025
-
The Energy Currency Used By Cells Is
Apr 06, 2025
-
How Tall Is 39 Inches In Feet
Apr 06, 2025
-
3 Letter Words Starting With I
Apr 06, 2025
-
What Is The Latin Word For Sour
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Does A Rhombus Have Point Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
