How Many Pairs Of Parallel Sides Does A Parallelogram Have
Juapaving
Mar 28, 2025 · 6 min read
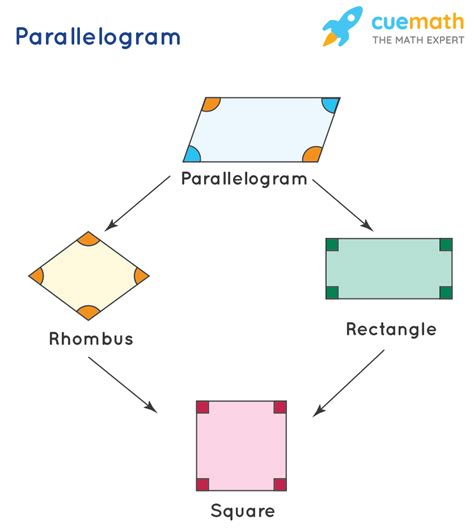
Table of Contents
How Many Pairs of Parallel Sides Does a Parallelogram Have? A Deep Dive into Parallelograms
Understanding the properties of geometric shapes is fundamental to various fields, from architecture and engineering to computer graphics and game development. Among the many shapes we encounter, the parallelogram holds a special place due to its unique characteristics. This article delves deep into the question: How many pairs of parallel sides does a parallelogram have? We'll explore the definition, properties, and applications of parallelograms, reinforcing the answer and solidifying your understanding of this important geometric figure.
Defining the Parallelogram
A parallelogram is a quadrilateral – a two-dimensional closed shape with four sides – where both pairs of opposite sides are parallel. This is the defining characteristic that sets a parallelogram apart from other quadrilaterals like rectangles, squares, rhombuses, and trapezoids. Understanding this definition is crucial to answering our central question. The parallelism of opposite sides is the key property that governs the other characteristics of a parallelogram.
Key Characteristics of a Parallelogram:
- Opposite sides are parallel: This is the fundamental characteristic, as already mentioned.
- Opposite sides are equal in length: The parallel sides are also congruent (equal in length).
- Opposite angles are equal: The angles opposite each other within the parallelogram are congruent.
- Consecutive angles are supplementary: This means that the sum of any two adjacent angles is 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at a point that divides each diagonal into two equal segments.
These properties are interconnected and derive directly from the fundamental property of parallel opposite sides. Let’s examine why this is so important.
Why the Parallelism Matters: Proof and Deduction
The statement that a parallelogram has one pair of parallel sides is incorrect. The very definition of a parallelogram explicitly states that it possesses two pairs of parallel sides. To understand why, let's consider a simple proof by contradiction.
Suppose we have a quadrilateral with only one pair of parallel sides. This shape is actually a trapezoid. A trapezoid is defined as a quadrilateral with at least one pair of parallel sides. If we were to assume a parallelogram only had one pair of parallel sides, we would be essentially describing a trapezoid, not a parallelogram. This contradiction proves that the assertion of only one pair of parallel sides for a parallelogram is false.
We can visually demonstrate this. Imagine drawing a parallelogram. You'll find it impossible to create a parallelogram where only one set of opposite sides runs parallel. Trying to force this will inevitably distort the shape, changing it from a parallelogram into something else, like a trapezoid.
This leads us to the definitive answer:
A parallelogram has two pairs of parallel sides.
Parallelograms vs. Other Quadrilaterals
Understanding the difference between a parallelogram and other quadrilaterals helps solidify our understanding of its defining properties. Let's compare it to some common related shapes:
- Rectangle: A rectangle is a parallelogram where all four angles are right angles (90 degrees). It retains the two pairs of parallel sides characteristic of the parallelogram, but adds the constraint of right angles.
- Square: A square is a special case of a rectangle (and therefore a parallelogram) where all four sides are equal in length. It still possesses two pairs of parallel sides, along with the right angles and equal side lengths.
- Rhombus: A rhombus is a parallelogram where all four sides are equal in length. While the side lengths are equal, the angles are not necessarily right angles. It maintains the crucial two pairs of parallel sides.
- Trapezoid (or Trapezium): As previously discussed, a trapezoid has only one pair of parallel sides. This distinguishes it clearly from a parallelogram.
This comparison highlights how the parallelogram serves as a parent shape for several other quadrilaterals, each with additional constraints or specific properties built upon the foundational characteristic of two pairs of parallel sides.
Real-World Applications of Parallelograms
Parallelograms are not just abstract geometric concepts; they find widespread applications in the real world. Their properties make them ideal for various practical uses:
- Architecture and Construction: Parallelograms appear in building designs, structural supports, and frameworks. The inherent stability of their parallel sides makes them suitable for load-bearing structures.
- Engineering: Many mechanical components, such as linkages and mechanisms, incorporate parallelogram structures to ensure smooth and predictable movement. The consistent parallel motion is crucial for reliable operation.
- Art and Design: Artists and designers utilize parallelograms in creating visual patterns, mosaics, and other artistic expressions. The symmetrical nature of parallelograms lends itself well to balanced compositions.
- Computer Graphics and Game Development: Parallelograms are fundamental shapes in computer graphics, used in creating 2D and 3D models, textures, and animations. Their properties make them efficient for rendering and manipulating images.
- Everyday Objects: Many everyday objects, from books and boxes to certain types of windows and furniture, incorporate parallelogram shapes either explicitly or implicitly in their design.
These are just a few examples demonstrating the practical relevance and widespread usage of parallelograms in diverse fields.
Further Exploration: Advanced Properties and Theorems
While the core property of two pairs of parallel sides is fundamental, parallelograms also possess several advanced properties that are worth exploring:
- Area Calculation: The area of a parallelogram is calculated by multiplying the base (length of one side) by the height (perpendicular distance between the parallel sides). This formula directly relates to the parallel sides' properties.
- Vector Representation: In linear algebra, parallelograms can be elegantly represented using vectors. The sides of the parallelogram can be represented as vectors, and the area can be calculated using the cross product of these vectors.
- Geometric Transformations: Parallelograms exhibit interesting properties under various geometric transformations like rotations, translations, and reflections. Understanding these transformations can deepen one's comprehension of their properties.
- Tessellations: Parallelograms can be used to create tessellations – repeating patterns that cover a surface without gaps or overlaps. This is because their parallel sides allow for seamless tiling.
Exploring these advanced properties enhances the understanding of parallelograms beyond their basic definition, showcasing their multifaceted nature and their connections to other mathematical concepts.
Conclusion: Reiterating the Core Concept
In conclusion, the unequivocal answer to the question, "How many pairs of parallel sides does a parallelogram have?" is two. This defining characteristic underpins all the other properties and applications of this important geometric shape. From its fundamental definition to its advanced properties and real-world applications, the parallelogram stands as a testament to the elegance and practicality of geometric principles. By understanding its properties, we unlock a deeper appreciation for the shapes that form the basis of our world.
Latest Posts
Latest Posts
-
What Is The Prime Factorization Of 420
Mar 31, 2025
-
Hansel And Gretel Short Story Pdf
Mar 31, 2025
-
Is There Friction In Outer Space
Mar 31, 2025
-
Formic Acid Is A Weak Acid
Mar 31, 2025
-
Mass Of An Electron In Mev
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Many Pairs Of Parallel Sides Does A Parallelogram Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
