How Many Lines Of Symmetry Are In A Regular Hexagon
Juapaving
Apr 05, 2025 · 6 min read
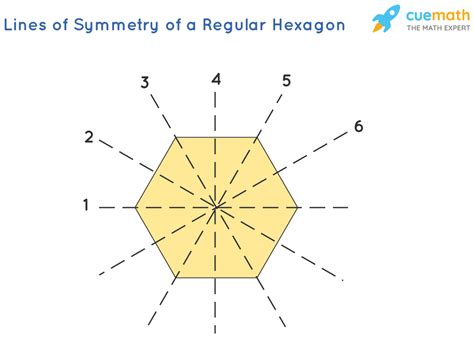
Table of Contents
How Many Lines of Symmetry Does a Regular Hexagon Have? A Comprehensive Exploration
Symmetry, a captivating concept in mathematics and geometry, refers to a balanced and proportionate arrangement of parts around a central point or axis. Understanding lines of symmetry is crucial in various fields, from art and design to architecture and engineering. This article delves deep into the fascinating world of symmetry, focusing specifically on the regular hexagon and the number of lines of symmetry it possesses. We will explore the concept of symmetry, define lines of symmetry, examine the properties of regular hexagons, and ultimately, determine the number of lines of symmetry present within this remarkable shape.
Understanding Symmetry and Lines of Symmetry
Before diving into the specifics of hexagons, let's establish a firm understanding of symmetry and lines of symmetry. Symmetry is a fundamental concept in geometry that describes the balanced distribution of shapes or patterns around a central point or axis. When a shape or object is symmetrical, it means that it can be divided into two or more identical parts that mirror each other.
A line of symmetry, also known as an axis of symmetry, is an imaginary line that divides a shape into two identical halves. If you were to fold the shape along this line, both halves would perfectly overlap. Shapes can possess multiple lines of symmetry, or none at all. The number of lines of symmetry depends on the shape's properties and its degree of regularity.
Properties of Regular Hexagons
A hexagon is a polygon with six sides and six angles. A regular hexagon, however, possesses specific properties that distinguish it from irregular hexagons. These properties are essential to determining its lines of symmetry. The key characteristics of a regular hexagon include:
- Equal side lengths: All six sides of a regular hexagon are equal in length.
- Equal angles: All six interior angles of a regular hexagon are equal, each measuring 120 degrees.
- Rotational symmetry: A regular hexagon exhibits rotational symmetry of order 6. This means it can be rotated about its center by multiples of 60 degrees and still appear identical.
These properties are crucial in understanding why a regular hexagon has the number of lines of symmetry it does. The regularity ensures a perfect balance and identical halves when folded along specific lines.
Identifying Lines of Symmetry in a Regular Hexagon
Let's visualize a regular hexagon and systematically identify its lines of symmetry. Imagine drawing lines through the hexagon, always ensuring the line divides the hexagon into two congruent (identical) halves.
We can identify three types of lines of symmetry in a regular hexagon:
-
Lines connecting opposite vertices: A regular hexagon has three lines of symmetry that connect opposite vertices (corners). These lines pass through the center of the hexagon, dividing it into two identical trapezoids. Each line creates a perfect mirror image on either side.
-
Lines bisecting opposite sides: Three additional lines of symmetry exist that bisect (divide into two equal parts) opposite sides of the hexagon. These lines also pass through the center, creating two identical shapes when the hexagon is folded along them.
The Total Number of Lines of Symmetry
Combining the lines connecting opposite vertices and the lines bisecting opposite sides, we arrive at the total number of lines of symmetry in a regular hexagon. There are three lines connecting opposite vertices and three lines bisecting opposite sides, resulting in a total of six lines of symmetry.
Therefore, a regular hexagon possesses six lines of symmetry. This high degree of symmetry is a direct consequence of its regular nature, with equal side lengths and equal angles. Any deviation from regularity would reduce the number of lines of symmetry.
Symmetry in Different Contexts: Examples and Applications
The concept of symmetry, and the understanding of lines of symmetry, extends far beyond the purely mathematical realm. It plays a significant role in various fields, including:
-
Art and Design: Artists and designers frequently utilize symmetry to create aesthetically pleasing and balanced compositions. Many works of art, from ancient mosaics to modern paintings, exhibit different types of symmetry. The use of symmetry can create a sense of order, harmony, and stability in a design.
-
Architecture and Engineering: Symmetrical structures are prevalent in architecture, providing stability and visual appeal. Buildings often incorporate symmetry in their design, reflecting a sense of balance and proportion. In engineering, understanding symmetry is crucial for structural analysis and design, ensuring stability and functionality. Bridges, for instance, often employ symmetrical designs for strength and balance.
-
Nature: Symmetry abounds in nature, appearing in various forms from snowflakes and flowers to animal bodies. The symmetrical patterns found in nature often reflect underlying mathematical principles, showcasing the elegant relationship between mathematics and the natural world. The hexagonal structure of honeycombs is a prime example of symmetry in nature, reflecting the bees' efficient use of space and materials.
-
Crystallography: The study of crystals relies heavily on the understanding of symmetry. Crystals often exhibit various types of symmetry, influencing their physical and chemical properties. Analyzing the symmetry of crystals helps determine their structure and properties.
Distinguishing Regular from Irregular Hexagons: Symmetry as a Defining Factor
It is crucial to distinguish between regular and irregular hexagons. While all hexagons have six sides, regular hexagons have equal side lengths and equal interior angles. Irregular hexagons, on the other hand, do not possess this regularity.
The number of lines of symmetry is a defining characteristic that distinguishes regular from irregular hexagons. A regular hexagon has six lines of symmetry, as previously established. An irregular hexagon, however, will have fewer lines of symmetry, or even none at all, depending on its specific shape.
Advanced Concepts: Symmetry Groups and Transformations
The concept of symmetry can be further explored through the study of symmetry groups and geometric transformations. A symmetry group is a mathematical group representing all the symmetries of a geometric object. Geometric transformations, such as reflections and rotations, are used to describe the symmetries of a shape.
Understanding symmetry groups allows a deeper analysis of the symmetries of a regular hexagon and other geometric shapes. It enables the classification and comparison of different types of symmetries and provides a more rigorous mathematical framework for understanding symmetry.
Conclusion: The Significance of Symmetry in a Regular Hexagon
The regular hexagon, with its six lines of symmetry, serves as a prime example of geometric symmetry. Its inherent balance and regularity have profound implications across various fields, from art and design to nature and engineering. Understanding the number of lines of symmetry in a regular hexagon highlights the importance of symmetry in mathematics and its widespread relevance in the world around us. By exploring this fundamental geometric concept, we gain a deeper appreciation for the beauty and order found in both mathematical constructs and natural phenomena. The six lines of symmetry in a regular hexagon aren't just a mathematical fact; they are a testament to the elegance and power of symmetry in shaping our world.
Latest Posts
Latest Posts
-
Type Of Energy Transformed By A Toaster Into Thermal Energy
Apr 06, 2025
-
Are All Angles Of A Parallelogram Congruent
Apr 06, 2025
-
What Is Not A Symptom Of Foodborne Illness
Apr 06, 2025
-
How Many Food Chains Make Up The Food Web
Apr 06, 2025
-
69 1 Liquid Measurement Ratio Calculator
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Are In A Regular Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
