Are All Angles Of A Parallelogram Congruent
Juapaving
Apr 06, 2025 · 5 min read
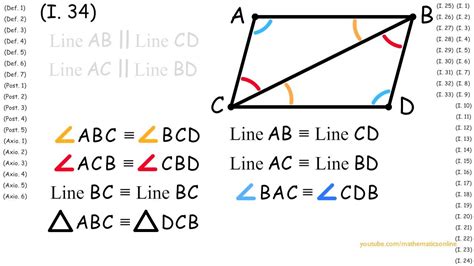
Table of Contents
Are All Angles of a Parallelogram Congruent? Exploring the Properties of Parallelograms
Are all angles of a parallelogram congruent? The short answer is no. While parallelograms possess many fascinating geometric properties, the congruence of all their angles is not one of them. However, understanding which angles are congruent and why is crucial to grasping the fundamental nature of parallelograms. This article delves deep into the properties of parallelograms, exploring their angles, sides, and diagonals to fully answer this question and illuminate the underlying geometric principles.
Understanding Parallelograms: A Definition and Basic Properties
A parallelogram is a quadrilateral – a four-sided polygon – with specific properties defining its shape and characteristics. These defining properties are:
- Opposite sides are parallel: This is the core defining characteristic. The opposite sides of a parallelogram are always parallel to each other. This parallelism is the foundation for many other properties.
- Opposite sides are congruent: Not only are opposite sides parallel, but they are also equal in length. This congruence is directly linked to the parallelism.
- Opposite angles are congruent: This is a key property relevant to our central question. While all angles aren't congruent, opposite angles are. This means that the angles diagonally opposite each other are equal in measure.
- Consecutive angles are supplementary: Consecutive angles are angles that share a common side. In a parallelogram, any two consecutive angles add up to 180 degrees (supplementary angles). This is a direct consequence of the parallel lines and transversal formed by the sides.
Why Not All Angles are Congruent: The Case for Supplementary Angles
Let's consider a simple example. Imagine a rectangle. A rectangle is a special type of parallelogram where all angles are right angles (90 degrees). In this specific case, all angles are congruent. However, this is not true for all parallelograms.
Consider a parallelogram that is not a rectangle – perhaps a tilted square, also known as a rhombus. In this case, the opposite angles are still equal, but the angles themselves are not all 90 degrees. Some angles will be acute (less than 90 degrees), and some will be obtuse (greater than 90 degrees). These acute and obtuse angles are supplementary to their adjacent angles, maintaining the 180-degree sum for consecutive angles.
This highlights a crucial distinction: While opposite angles in a parallelogram are always congruent, consecutive angles are supplementary but not congruent (unless the parallelogram is a rectangle).
Exploring Special Cases: Rectangles, Rhombuses, and Squares
The relationship between angles in a parallelogram becomes clearer when we examine special cases of parallelograms:
Rectangles: A Parallelogram with Congruent Angles
A rectangle is a parallelogram where all four angles are right angles (90 degrees). Therefore, in a rectangle, all angles are congruent. This is a unique characteristic of rectangles within the broader family of parallelograms.
Rhombuses: A Parallelogram with Congruent Adjacent Sides
A rhombus is a parallelogram with all four sides congruent. While opposite angles are congruent, adjacent angles are supplementary but not necessarily congruent. Only in the special case of a square (which is both a rhombus and a rectangle) are all angles congruent.
Squares: The Perfect Parallelogram
A square is a special case where it's both a rectangle and a rhombus. This means it possesses all the properties of both: all sides are congruent, and all angles are congruent (90 degrees). The square represents the unique situation where the parallelogram’s angles are all congruent.
Proving the Properties: Geometric Demonstrations
The properties of parallelograms, including the congruence of opposite angles and the supplementary nature of consecutive angles, can be rigorously proven using geometric principles.
One common approach involves using the properties of parallel lines and transversals. Drawing a diagonal within the parallelogram creates two triangles. Using alternate interior angles theorem (angles formed by a transversal crossing parallel lines), we can prove that opposite angles are congruent. Similarly, using the linear pair theorem (angles that form a straight line add to 180 degrees), we can prove that consecutive angles are supplementary.
These proofs depend on the fundamental axioms and postulates of Euclidean geometry. They provide a solid mathematical foundation for understanding why a parallelogram has the properties it does, clarifying why only opposite angles are congruent.
Real-World Applications: Parallelograms in Architecture and Engineering
Parallelograms are not just abstract geometric shapes; they have numerous practical applications in various fields. Their inherent stability and predictable properties make them valuable in:
- Architecture and Construction: Parallelogram-shaped structures offer strength and efficiency. The parallelogram's ability to distribute weight evenly makes it suitable for load-bearing structures and designs.
- Engineering: In mechanical engineering, parallelogram mechanisms are used to create linear motion from rotational motion. This is crucial in various machines and devices.
- Art and Design: Parallelograms are employed in artistic and design contexts, creating visual interest and balance in compositions.
Distinguishing Parallelograms from Other Quadrilaterals
It's crucial to differentiate parallelograms from other quadrilaterals such as trapezoids, kites, and irregular quadrilaterals. Trapezoids have only one pair of parallel sides, while kites have two pairs of adjacent congruent sides. Irregular quadrilaterals lack any specific relationships between their sides or angles. Understanding these differences is essential to correctly identifying and analyzing geometric shapes.
Advanced Concepts and Extensions: Vectors and Transformations
The properties of parallelograms can be further explored using vector algebra and geometric transformations. Vectors can be used to represent the sides of a parallelogram, and their properties can be used to derive the parallelogram's characteristics. Geometric transformations, such as translations, rotations, and reflections, can be applied to parallelograms to analyze their invariance and symmetries.
Conclusion: A Deep Dive into Parallelogram Geometry
In summary, while a rectangle (a specific type of parallelogram) has all congruent angles, not all parallelograms share this property. Only the opposite angles of a parallelogram are congruent. Consecutive angles, however, are always supplementary, adding up to 180 degrees. Understanding this distinction is key to mastering the fundamental properties of parallelograms and their place within the broader world of geometry. The exploration of parallelograms extends beyond basic geometry, finding application in advanced mathematical concepts and diverse practical applications. By understanding their unique characteristics, we gain valuable insights into the fascinating world of shapes and their properties.
Latest Posts
Latest Posts
-
Simplify The Square Root Of 121
Apr 08, 2025
-
Adjective That Starts With N To Describe A Mom
Apr 08, 2025
-
How Do Humans And Other Consumers Obtain Nitrogen
Apr 08, 2025
-
1200 Square Feet To Square Meters
Apr 08, 2025
-
How To Find The Distance Between Two Parallel Lines
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Are All Angles Of A Parallelogram Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.